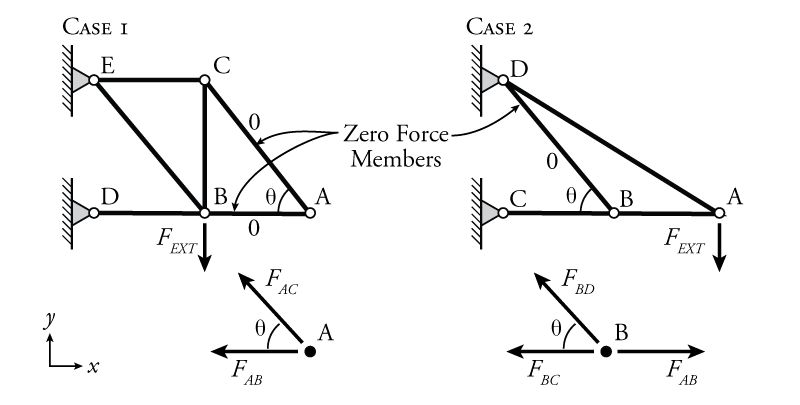
Zero force members in a truss are members which do not have any force in them (obviously...). There are two rules that may be used to find zero-force members in a truss. These are described below and illustrated in Figure 3.3.
- Case 1
- At a TWO member joint: If those members are NOT parallel AND there are no other external loads (or reactions) at the joint THEN both of those members are zero force members.
- Case 2
- In a THREE member joint: If TWO of those members ARE parallel AND there are no other external loads (or reactions) at the joint THEN the member that is not parallel is a zero force member.
Two examples, one for each case, are shown in Figure 3.3. By applying equilibrium to the appropriate joints, we can see why the members shown do not have any force.
For the case 1 example, members AB and AC are zero force members. This may be shown to be the case by solving the equilibrium equations \eqref{eq:TrussEquil} at joint A.
\begin{equation}\label{eq:TrussEquil} \tag{1} \sum_{i=1}^{n}{F_{xi}} = 0; \sum_{i=1}^{p}{F_{yi}} = 0; \end{equation}
For vertical equilibrium ($y$-direction), the vertical component of $F_{AC}$ is the only vertical force:
\begin{align*} F_{ACy} &= F_{AC} \sin \theta \\ \sum_{i=1}^{p}{F_{yi}} &= 0 \\ \therefore F_{ACy} &= 0 \\ F_{AC} \sin \theta &= 0 \\ \therefore F_{AC} &= 0 \text{ as long as } \theta \neq 0 \end{align*}
Therefore $F_{AC}$ is a zero-force member. If we now apply horizontal equilibrium ($x$-direction), we have two horizontal forces, $F_{AB}$ and the horizontal component of $F_{AC}$:
\begin{align*} F_{ACx} &= F_{AC} \cos \theta = 0 \\ \sum_{i=1}^{n}{F_{xi}} &= 0 \\ \therefore - F_{ACx} - F_{AB} &= 0 \\ F_{AB} &= - F_{ACx} = 0 \end{align*}
Therefore, $F_{AB}$ must also be a zero force member. In this example $F_{ACx}$ and $F_{AB}$ are both negative because the arrows both point to the left. This analysis works for any two loads at joint which are not parallel where there is no external load on the joint.
For case 2 in Figure 3.3, member BD is a zero force member. This may be shown to be the case by solving the equilibrium equations \eqref{eq:TrussEquil} at joint B. For vertical equilibrium, the vertical component of $F_{BD}$ is the only vertical force:
\begin{align*} F_{BDy} &= F_{BD} \sin \theta \\ \sum_{i=1}^{p}{F_{yi}} &= 0 \\ \therefore F_{BDy} &= 0 \\ F_{BD} \sin \theta &= 0 \\ \therefore F_{BD} &= 0 \text{ as long as } \theta \neq 0 \end{align*}
Therefore $F_{BD}$ is a zero-force member. This analysis was simplified because the members BC and AB were parallel to the $x$-axis; however, the orientation of the $x$-axis is arbitrary, an analysis will show that member BD is a zero force member as long as two of the members are parallel at the joint, even if they are not parallel to the $x$- or $y$-axis (try it out!).
Finding these zero force members up front can save analysis time and effort.
 Learn About Structures
Learn About Structures