When doing structural analysis, we often conceptualize a real structure as a simplified stick model with elements connected to each other at specific locations called nodes. Although the elements have deformations between the nodes, we can, using structural analysis methods, characterize the behaviour and deformation of the structure based on the deformations at the nodes alone.
A degree-of-freedom (or DOF) represents a single direction that a node is permitted to move or rotate. This concept was previously briefly introduced in Section 1.5. In a 2D system, each node has three possible degrees-of-freedom: translation (movement) in one direction, translation in another direction perpendicular to the first one, and rotation. Usually, we consider the horizontal and vertical axes as the two perpendicular translational degrees-of-freedom. Although three DOFs are possible for each node, individual directions may be considered to be restrained, either by a support reaction or by one of the members connected to the node.
In a slope-deflection method analysis, we will typically make the assumption that all frame members are axially rigid for the purpose of determining the number of degrees of freedom in the system (i.e. we assume that the beams cannot elongate or compress). This is usually a good assumption for beam and frame analysis since the structural deformations are mostly caused by bending of frame elements, not axial elongation. By making this assumption, we reduce the number of effective DOFs in the slope-deflection analysis and, therefore, reduce the number of equations in the system of equations that we have to solve.
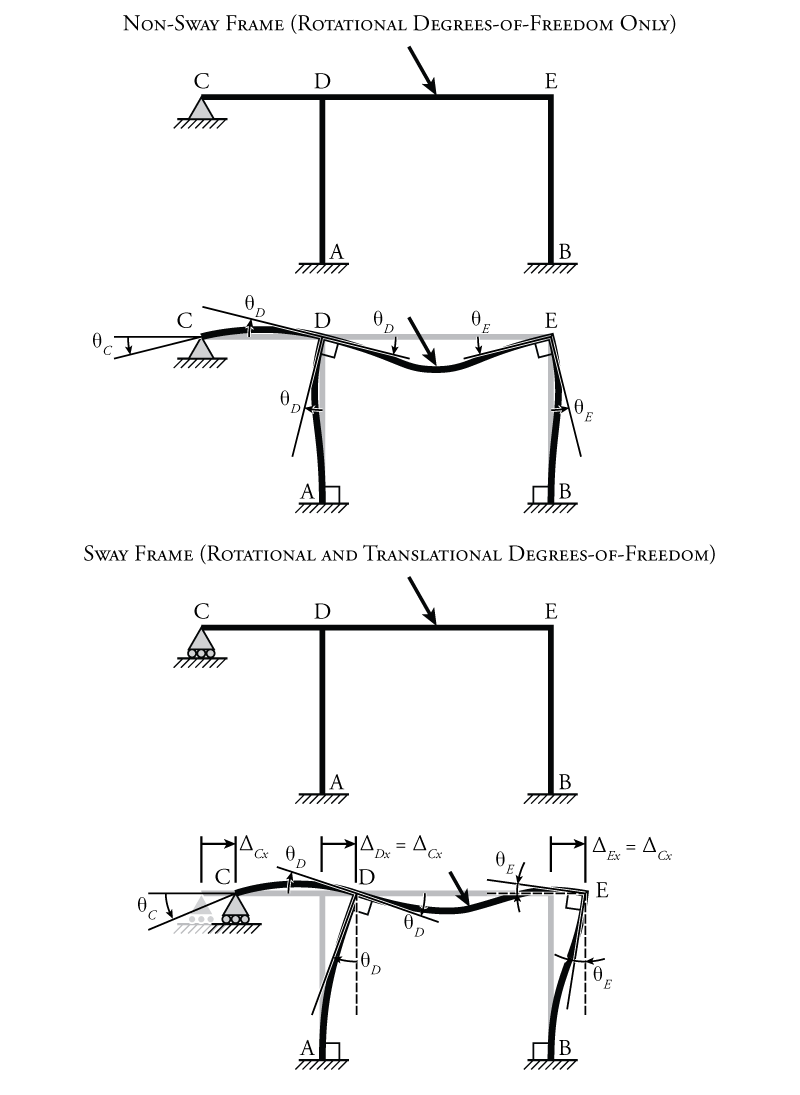
A simple example is shown at the top of Figure 9.1 (labelled 'Non-Sway Frame'). In this frame structure, we can look at each node individually to evaluate the total number of degrees of freedom in our system:
- Nodes A and B
- cannot translate (displace) horizontally or vertically and cannot rotate because of the fixed end supports at those locations. (Total free DOFs = 0)
- Node C
- cannot translate (displace) either horizontally or vertically because of the pin at that location. It can rotate, and will have a rotation of $\theta_C$ as shown in the figure. (Total free DOFs = 1)
- Node D
- cannot translate horizontally due to the restraint provided by member CD which is restrained horizontally by the pin at point C (recall that we are considering the frame members to be rigid axially). Node D cannot translate vertically due to the restraint provided by member AD which is restrained vertically by the fixed end at node A. It can rotate, and will have a rotation of $\theta_D$ as shown in the figure. The same rotation is applied to the ends of all three members that frame into node D (AD, CD, and DE). (Total free DOFs = 1)
- Node E
- cannot translate horizontally due to the restraint provided by member DE which is restrained horizontally by member CD which is restrained horizontally by the pin at point C. Node E cannot translate vertically due to the restraint provided by member BE which is restrained vertically by the fixed end at node B. It can rotate, and will have a rotation of $\theta_E$ as shown in the figure. The same rotation is applied to the ends of both members that frame into node E (BE and DE). (Total free DOFs = 1)
Adding up all of the DOFs for each node, we see that this structure has three total DOFs: $\theta_C$, $\theta_D$, and $\theta_E$. So, for a slope-deflection method analysis, we would need to solve a system of three equations and three unknowns. Since one of the member ends has a pin support (at node C), we will be able to use a special formulation for the slope-deflection equations to reduce the number of equations to two (as we will see). This is an easy problem to solve by hand. If we used the force method to analyse this structure, we will have to solve a system of five equations and five unknowns since the structure is ${5^\circ}$ indeterminate. This would be all but impossible to do by hand.
Since there are only rotational DOFs in this structure, and no translational DOFs (i.e. all nodes remain at the same points in space), then this top structure shown in Figure 9.1 is considered to be a non-sway frame. In contrast, a sway frame is a structure where any of the joints can translate or displace. The non-sway frame may be converted into a sway frame by removing the horizontal restraint at point C (converting the pin into a roller). The resulting structure is shown in the lower half of Figure 9.1.
We can again look at each node individually for the sway frame in Figure 9.1 to evaluate the total number of degrees of freedom in our system:
- Nodes A and B
- still cannot translate (displace) horizontally or vertically and cannot rotate because of the fixed end supports at those locations. (Total free DOFs = 0)
- Node C
- cannot translate (displace) vertically because of the roller at that location; however it can now translate horizontally since no horizontal restraint is provided by the support or by the member CD. This horizontal translation may be called $\Delta_{Cx}$ as shown in the figure. The node can also rotate, and will have a rotation of $\theta_C$ as shown in the figure. (Total free DOFs = 2)
- Node D
- cannot translate vertically due to the restraint provided by member AD which is restrained vertically by the fixed end at node A; however, it can now translate horizontally since no horizontal restraint is provided by member CD anymore. This horizontal translation may be called $\Delta_{Dx}$ as shown in the figure; however, since member CD is still axially rigid, the translation $\Delta_{Dx}$ in the horizontal direction must be exactly equal to the horizontal translation of point C ($\Delta_{Cx}$). Since both points C and D move together, they are considered together to represent only a single DOF (they are not independent of each other). So no new DOF is added to the system due to the horizontal translation of point D. Node D can rotate, and will have a rotation of $\theta_D$ as shown in the figure (which is a new independent DOF). (Total free DOFs = 2, Total Independent free DOFs = 1)
- Node E
- cannot cannot translate vertically due to the restraint provided by member BE which is restrained vertically by the fixed end at node B. Like node D, node E can now translate horizontally ($\Delta_{Ex}$ as shown in the figure), but the amount of horizontal translation is equal to the horizontal translation of points C and D ($\Delta_{Cx}$ and $\Delta_{Dx}$), so this does not constitute a new independent DOF. Node E can rotate, and will have a rotation of $\theta_E$ as shown in the figure (which is a new independent DOF). (Total free DOFs = 2, Total Independent free DOFs = 1)
Adding up all of the DOFs for each node, we see that this structure has four total independent DOFs: $\Delta_{Cx}$, $\theta_C$, $\theta_D$, and $\theta_E$. So, for a slope-deflection method analysis, we would need to solve a system of four equations and four unknowns, but again we will be able to use a special formulation for the slope-deflection equations to reduce the number of equations to three (as we will see).
 Learn About Structures
Learn About Structures