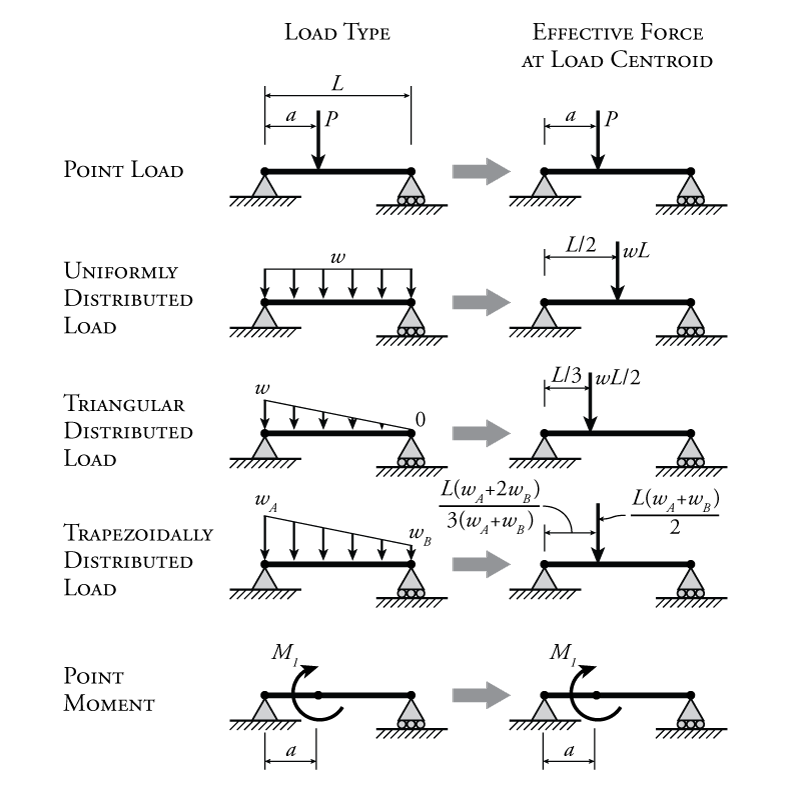
A number of common loading types for beams and frames are shown in Figure 4.1. This is not an exhaustive list, but shows all the types of loads that we will deal with in this book. Out of these, by far the most common are the top two, point load and uniformly distributed load. The point load is just a single force acting on a single point on a beam or frame member. The uniformly distributed load, also just called a uniform load is a load that is spread evenly over some length of a beam or frame member. In structures, these uniform loads usually come from area loads acting across the face of a floor or wall which must be resisted by a connected beam or column. This area load is multiplied by a tributary width, usually the distance between adjacent beams or columns, to convert the area load to a the uniform line load like the one shown in the figure. These uniform loads are given in units of force per unit distance (for example kN/m). In addition to the uniform load, load may be distributed on structural members in other ways, such as the triangular or trapezoidal distributed loads shown in Figure 4.1 (among others). We will also encounter point moments as shown in the figure. These point moments may often be caused by other members or elements that are connected to the beam or frame member which are not included directly in the free body diagram. More commonly, you will encounter point moments at fixed end reaction locations.
How can we deal with these types of uniform or other distributed loads when performing equilibrium calculations? The way to do this is to consider a equivalent total load or effective force caused by the distributed load, which acts at the centroid of the distribution. The location of this centroid is different depending on the type of load distribution as shown on the right side of Figure 4.1. For a uniform load, the effective force is equal to the total load given by the load per unit length multiplied by the total length (or $wL$). This is also equal to the area under the distributed load diagram, in this case a rectangle. For the uniform load, the centroid is at the center of the distribution ($L/2$). This is the location where you would put the effective force in order to use it in equilibrium calculations. For the triangular load, the effective load is again the total load which is equal to the area under the distribution, in this case $wL/2$ ($\frac{1}{2}bh$) and this acts at the centroid of the triangle, which is located at one-third of the length from the high side. For the trapezoidally distributed load, the case is slightly more complex as shown in Figure 4.1.
The point load and point moment do not have any equivalent total load, since they already act at a single point.
 Learn About Structures
Learn About Structures