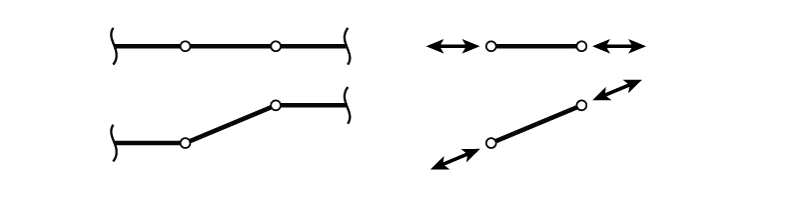
Trusses are structures that only use members that may be considered to have pinned connections at either end. This means that the members can only take axial load (not moment or shear) as shown in Figure 3.1. When the ends of the truss member shown in the figure move, they may have the effect of rotating the member (since the ends are pinned, they are free to rotate), but will not cause any bending or shear. The member will remain straight because of the pins/hinges at either end. Therefore the only load in the element can be axial load as shown on the right side of the figure.

Figure 3.1: Truss Member Showing Pinned Connections to the Surrounding Structure

Since a truss element can only transmit axial force, and not moment or shear, there are only two useful equilibrium equations for the analysis of individual truss members and joints:

\begin{equation}\label{eq:TrussEquil} \sum_{i=1}^{n}{F_{xi}} = 0; \sum_{i=1}^{p}{F_{yi}} = 0; \end{equation}

or, in a more simplified form:

\begin{equation} \boxed{ \sum F_x = 0; \sum F_y = 0 \, } \end{equation}

+Moment equilibrium at the joint still applies; however, it is not useful because we already know that a truss member cannot apply a moment to a joint and vice-versa, making the moment contribution from each member equal to zero ($\sum_{i=1}^{n}{M_i}= \sum_{i=1}^{n}{0} = 0$).

There are two common ways to analyse determinate truss systems, the method of joints or the method of sections. Without any additional analysis tools, these methods may only be used to analyse determinate trusses. Evaluating the determinacy of trusses was previously discussed in Section 2.5. Analysis of indeterminate trusses will be described Chapter 8.