Recall again the slope deflection equations from Section 9.3.
\begin{equation} \boxed{ M_{AB} = \frac{2EI}{L} (2 \theta_A + \theta_B - 3 \psi ) + \text{FEM}_{AB} } \label{eq:SD-AB} \tag{1} \end{equation} \begin{equation} \boxed{ M_{BA} = \frac{2EI}{L} (\theta_A + 2 \theta_B - 3 \psi ) + \text{FEM}_{BA} } \label{eq:SD-BA} \tag{2} \end{equation} \begin{equation} \boxed{ M_{nf} = \frac{2EI}{L} (2 \theta_n + \theta_f - 3 \psi ) + \text{FEM}_{nf} } \label{eq:SD-NF} \tag{3} \end{equation} \begin{equation} \boxed{ M_{rh} = \frac{3EI}{L} (\theta_r - \psi ) + \left( \text{FEM}_{rh} - \frac{\text{FEM}_{hr}}{2} \right) } \label{eq:SD-RH} \tag{4} \end{equation} \begin{equation} \boxed{ M_{hr} = 0 } \label{eq:SD-HR} \tag{5} \end{equation}
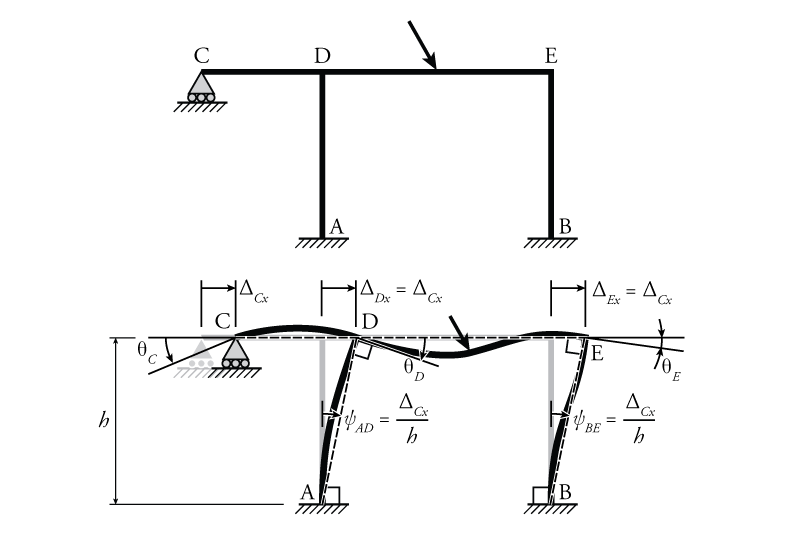
Recall that a sway frame is simply a frame that has translational in addition to rotational degrees of freedom. Consider the example sway frame shown in Figure 9.18 (this is the same sway frame that was previously shown in Figure 9.1). This frame has four total independent degrees-of-freedom: the rotations at nodes C, D and E ($\theta_C$, $\theta_D$ and $\theta_E$ as shown in the figure) plus the horizontal translation of the top beam ($\Delta_{Cx}$). The beam CDE only has one horizontal translational DOF because we are assuming that all members are axially rigid, as previously discussed. So, the horizontal translation at D ($\Delta_{Dx}$) and at E ($\Delta_{Ex}$) are both identical, and therefore not independent of the horizontal translation at point C ($\Delta_{Cx}$). The vertical translation of node C is restrained by the support at C, the vertical translation of nodes D and E are restrained by members AD and BE, respectively, which both have fixed ends at their bases. The four total independent degrees-of-freedom may be reduced to three effective degrees-of-freedom for a slope-deflection analysis by using equation \eqref{eq:SD-RH} instead of equation \eqref{eq:SD-NF} for member CD (since we know that the moment will be zero at the pinned end C).
So, we need some way to bring the DOF $\Delta_{Cx}$ into our equilibrium equations. We can do that using the chord rotation parameter that is already a part of the slope-deflection equations ($\psi$). In the sample structure from Figure 9.18, the horizontal translation $\Delta_{Cx}$ will cause chord rotations for members AD and BE as shown. Recall that the chord is a straight line drawn between the two ends of a member and the rotation of a chord is given by the equation:
\begin{align} \psi = \frac{\Delta}{L} \tag{6} \end{align}
or in this case:
\begin{align} \psi_{AD} = \psi_{BE} = \frac{\Delta_{Cx}}{h} \tag{7} \end{align}
In this case, the chord rotation caused by the horizontal translation degree-of-freedom is the same for both members AD and BE (because they happen to be the same length and also have the save deviation $\Delta_{Cx}$).
The problem now is that, although we have three unknowns (unknown DOFs) $\theta_D$, $\theta_C$ and $\Delta_{Cx}$, we still only the have two moment equilibrium equations for nodes D and E:
\begin{align} M_{DA} + M_{DC} + M_{DE} &= 0 \tag{8} \\ M_{EB} + M_{ED} &= 0 \tag{9} \end{align}
We need some third equation to use. For this third equation we can use a global equilibrium equation. It is often convenient for a frame analysis like this one to use the global horizontal equilibrium for the frame.e
To calculate the global horizontal equilibrium for the entire frame, we need to know all of the horizontal reaction forces. For this case, the horizontal reaction forces at points A and B will be equal to the shear forces at the bottom ends of members AD and BE ($V_{AD}$ and $V_{BE}$), as shown in Figure 9.19. But, since our slope-deflection equations are in terms of end moments only (not shears) we would prefer to have the shears in terms of the end moments. We can find the shears at the bottom ends of member AD and BE in terms of the end moments in those members by applying local equilibrium for each member as shown on the lower half of Figure 9.19.
For the example structure shown in Figure 9.19, we can find the shear at node A of member AD by taking a moment equilibrium about point D:
\begin{align} \curvearrowleft \sum M_{D} &= 0 \tag{10} \\ M_{DA} + M_{AD} + V_{AD} (h) &= 0 \tag{11} \\ V_{AD} &= -\frac{M_{DA} + M_{AD}}{h} \tag{12} \end{align}
Likewise for member EB, the shear at the base (node B) is:
\begin{align} V_{BE} &= -\frac{M_{EB} + M_{BE}}{h} \tag{13} \end{align}
These shears are equivalent to the horizontal reaction forces at nodes A and B. So if we now take a global horizontal equilibrium for the entire structure (represented in the top half of Figure 9.19): \begin{align} \rightarrow \sum F_x &= 0 \tag{14} \\ P \cos \theta + V_{AD} + V_{BE} &= 0 \tag{15} \\ P \cos \theta -\frac{M_{DA} + M_{AD}}{h} - \frac{M_{EB} + M_{BE}}{h} &= 0 \tag{16} \\ Ph \cos \theta - M_{DA} - M_{AD} - M_{EB} - M_{BE} &= 0 \tag{17} \end{align}
This last equation represents an additional equilibrium equation for the structure. This is a useful equilibrium equation because it is only a function of the known external forces (in this case $P$) and the member end moments, which we can find expressions for using the slope-deflection equation.
So, to summarize, the three equilibrium equations for the structure shown in Figure 9.18 are:
\begin{align} M_{DA} + M_{DC} + M_{DE} &= 0 \tag{18} \\ M_{EB} + M_{ED} &= 0 \tag{19} \\ Ph \cos \theta - M_{DA} - M_{AD} - M_{EB} - M_{BE} &= 0 \tag{20} \end{align}
The rest of the slope-deflection analysis is the same as before: find the end moments using the slope deflection equations (including consideration of fixed and moments and chord rotations), substitute these into the equilibrium equations, solve the equilibrium equations for the unknown DOF rotations and translations, and then sub these back into the end moment equations.
Example
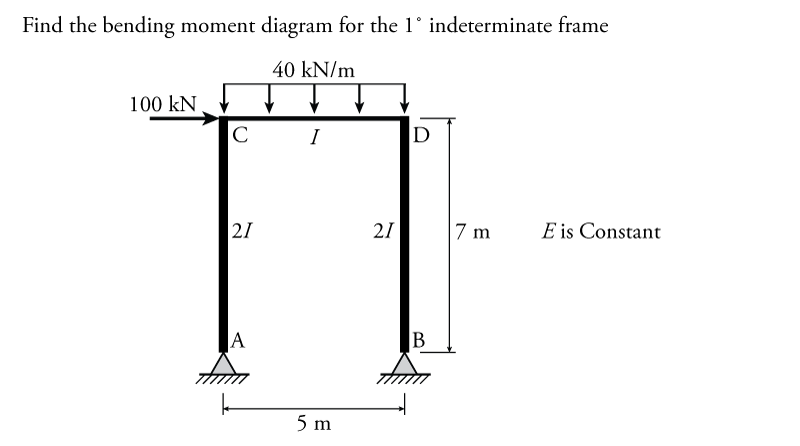
The slope-deflection method for sway frames will be illustrated using the example structure shown in Figure 9.20. This is a simple portal frame structure with pinned column bases. There is a uniformly distributed load on the top beam (member CD) and a single lateral (horizontal load) at node C. The Young's Modulus $E$ is constant for all members and the columns have twice the moment of inertia $I$ as the beam.
The degrees-of-freedom and chord rotations for the example structure are shown in Figure 9.21. This structure has five independent degrees of freedom, the rotations at every node ($\theta_A$, $\theta_B$, $\theta_C$ and $\theta_D$) plus the horizontal translation of the beam $\Delta_{Cx}$. The horizontal translations of nodes C and D are coupled by the member CD (which we consider to be axially rigid). This means that $\Delta_{Dx}$ is equal to $\Delta_{Cx}$ and so is not an independent DOF for this structure.
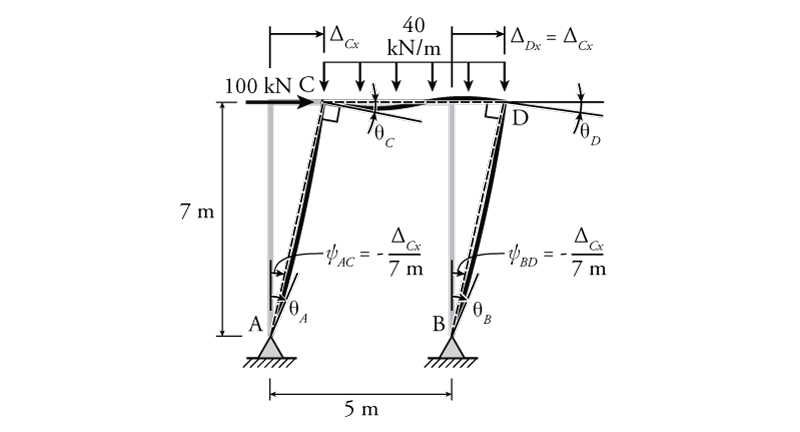
The five total independent degrees-of-freedom may be reduced to three effective degrees-of-freedom for a slope-deflection analysis by using equation \eqref{eq:SD-RH} instead of equation \eqref{eq:SD-NF} for members AC and BD (since we know that the moment will be zero at the pinned ends at nodes A and B).
First, let's find the necessary equilibrium equations. We will need three equilibrium equations since we have three independent unknowns. Two of these come directly from the moment equilibrium at nodes C and D:
\begin{align*} M_{CA} + M_{CD} &= 0 \\ M_{DC} + M_{DB} &= 0 \end{align*}
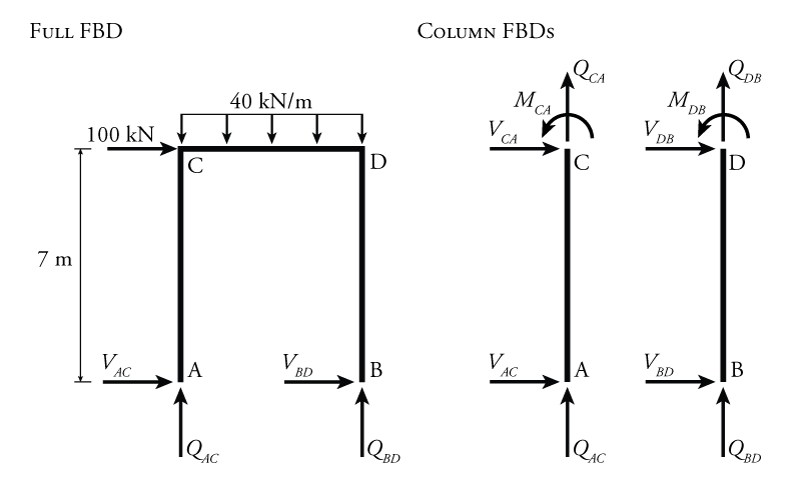
The third equilibrium condition will come from the global horizontal equilibrium of the entire structure as shown in Figure 9.22. By applying moment equilibrium at the top of each column, the shear at the base of each column is equal to:
\begin{align*} V_{AC} &= - \frac{M_{CA}}{7} \\ V_{BD} &= - \frac{M_{DB}}{7} \end{align*}
Applying global equilibrium to the left diagram in Figure 9.22 (the entire structure), we get:
\begin{align*} 100 + V_{AC} + V_{BD} &= 0 \\ 100 - \frac{M_{CA}}{7} - \frac{M_{DB}}{7} &= 0 \\ M_{CA} + M_{DB} - 700 &= 0 \end{align*}
This last equation is our third equilibrium equation for this problem.
The next step is to use the slope-deflection equations to find the end moments at either end of each member. For these, we need to first determine the chord rotations and the fixed end moments.
While there are no support settlements in this example, the sway of the frame (the translation $\Delta_C$) causes chord rotations for members AC and BD, as previously shown in Figure 9.21. The resulting chord rotations are:
\begin{align*} \psi_{AC} = \psi_{BD} = -\frac{\Delta_{Cx}}{7} \end{align*}
The chord rotation is negative because it's clockwise. Unlike the support settlement case, where we generally know the value of the displacement $\Delta$, in the sway frame case the $\Delta_{Cx}$ is an unknown DOF translation that we are trying to find. Therefore the variable $\Delta_{Cx}$ will carry through the slope-deflection equations and be present in the equilibrium conditions at the end of the analysis.
There is only one member in the example structure that has loads applied between the end nodes, member CD (see Figure 9.20). The fixed end moments for this member, based on the values in Figure 9.6, are:
\begin{align*} \text{FEM}_{CD} &= \frac{wL^2}{12} \\ \text{FEM}_{CD} &= \frac{40(5)^2}{12} \\ \text{FEM}_{CD} &= +83.3\mathrm{\,kNm} \curvearrowleft \\ \text{FEM}_{DC} &= -83.3\mathrm{\,kNm} \curvearrowright \end{align*}
None of the other members have fixed end moments, so:
\begin{align*} \text{FEM}_{AC} = \text{FEM}_{CA} = \text{FEM}_{BD} = \text{FEM}_{DB} = 0 \end{align*}
Now that we know all of the inputs for the slope-deflection equations, we can find the end moments for each member. Since members AC and BD have pinned ends at their base nodes (nodes A and B), we know there must be zero moment at those locations. Therefore, we can use the slope-deflection equations \eqref{eq:SD-RH} and \eqref{eq:SD-HR} to save work by eliminating the need to consider the rotations at nodes A and B (instead of the more general form of the slope-deflection equation \eqref{eq:SD-NF}). For member AC:
\begin{align*} M_{rh} &= \frac{3EI}{L} (\theta_r - \psi ) + \left( \text{FEM}_{rh} - \frac{\text{FEM}_{hr}}{2} \right) \\ M_{hr} &= 0 \end{align*}
For the end moments in member AC, A is the hinge side ($h$) and C is the rigid side ($r$), so:
\begin{align*} M_{CA} &= \frac{3EI}{L} (\theta_C - \psi_{AC} ) + \left( \text{FEM}_{CA} - \frac{\text{FEM}_{AC}}{2} \right) \\ M_{AC} &= 0 \end{align*}
Substituting in the known values for the chord rotations and fixed end moments (not forgetting that member AC has a moment of inertia of $2I$):
\begin{align*} M_{CA} &= \frac{3E(2I)}{7} \left( \theta_C - \left( -\frac{\Delta_{Cx}}{7} \right) \right) + \left( 0 - 0 \right) \end{align*}
Therefore,
\begin{equation*} \boxed{M_{AC} = 0 } \end{equation*} \begin{equation*} \boxed{M_{CA} = 0.858 EI \theta_C + 0.1714 EI \Delta_{Cx} } \end{equation*}
Similarly, member BD also has a pinned end with zero moment and may therefore use the slope-deflection equations \eqref{eq:SD-RH} and \eqref{eq:SD-HR}:
\begin{align*} M_{DB} &= \frac{3EI}{L} (\theta_D - \psi_{BD} ) + \left( \text{FEM}_{DB} - \frac{\text{FEM}_{BD}}{2} \right) \\ M_{BD} &= 0 \end{align*}
Substituting known values (again not forgetting that member BD has a moment of inertia of $2I$):
\begin{align*} M_{DB} &= \frac{3E(2I)}{7} \left( \theta_D - \left( -\frac{\Delta_{Cx}}{7} \right) \right) + \left( 0 - 0 \right) \\ \end{align*}
Therefore,
\begin{equation*} \boxed{M_{BD} = 0 } \end{equation*} \begin{equation*} \boxed{M_{DB} = 0.858 EI \theta_D + 0.1714 EI \Delta_{Cx} } \end{equation*}
Member CD has two continuous ends that can transfer moment, so it will have non-zero moments at both ends and we must use slope-deflection equation \eqref{eq:SD-NF}:
\begin{align*} M_{nf} &= \frac{2EI}{L} (2 \theta_n + \theta_f - 3 \psi ) + \text{FEM}_{nf} \end{align*}
For the moment at the end of member CD at node C, C is the near side and D is the far side, so:
\begin{align*} M_{CD} &= \frac{2EI}{L} (2 \theta_C + \theta_D - 3 \psi_{CD} ) + \text{FEM}_{CD} \\ M_{CD} &= \frac{2EI}{5} (2 \theta_C + \theta_D - 3 (0) ) + 83.3 \end{align*} \begin{equation*} \boxed{M_{CD} = 0.8EI \theta_C + 0.4 EI \theta_D + 83.3 } \end{equation*}
Likewise for node D:
\begin{align*} M_{DC} &= \frac{2EI}{L} (2 \theta_D + \theta_C - 3 \psi_{CD} ) + \text{FEM}_{DC} \\ M_{DC} &= \frac{2EI}{5} (2 \theta_D + \theta_C - 3 (0) ) - 83.3 \end{align*} \begin{equation*} \boxed{M_{DC} = 0.8EI \theta_D + 0.4 EI \theta_C - 83.3 } \end{equation*}
These six end moments may then be substituted into the equilibrium conditions:
\begin{align*} M_{CA} + M_{CD} &= 0 \\ M_{DC} + M_{DB} &= 0 \\ M_{CA} + M_{DB} - 700 &= 0 \end{align*}
to get:
\begin{align*} 1.658 EI \theta_C + 0.4 EI \theta_D + 0.1714 EI \Delta_{Cx} + 83.3 &= 0 \\ 0.4 EI \theta_C + 1.658 EI \theta_D + 0.1714 EI \Delta_{Cx} - 83.3 &= 0 \\ 0.858 EI \theta_C + 0.858 EI \theta_D + 0.3428 EI \Delta_{Cx} - 700 &= 0 \end{align*}
These three independent equilibrium equations may be solved for the three DOF unknowns $\theta_C$, $\theta_D$ and $\Delta_{Cx}$ in terms of EI to get:
\begin{align*} EI \theta_C &= -357.9\mathrm{\,kNm^2} \\ EI \theta_D &= -225.5\mathrm{\,kNm^2} \\ EI \Delta_{Cx} &= 3502.0\mathrm{\,kNm^3} \end{align*}
Often, it may be convenient to keep these values in terms of $EI$ multiplied by the DOF rotation or translation because the $EI$ will cancel out when we substitute these back into the slope-deflection-derived end moment expressions. In this example, we cannot find the actual values for the rotations and translations since we are not given $EI$.
Now using the known DOF rotations and translations $\theta_C$, $\theta_D$ and $\Delta_{Cx}$, we can solve for the value of each end moment using the previously constructed slope-deflection end moment expressions to get:
\begin{align*} M_{AC} &= 0 \\ M_{CA} &= +293\mathrm{\,kNm} \curvearrowleft \\ M_{BD} &= 0 \\ M_{DB} &= +407\mathrm{\,kNm} \curvearrowleft \\ M_{CD} &= -293\mathrm{\,kNm} \curvearrowright \\ M_{DC} &= -407\mathrm{\,kNm} \curvearrowright \end{align*}
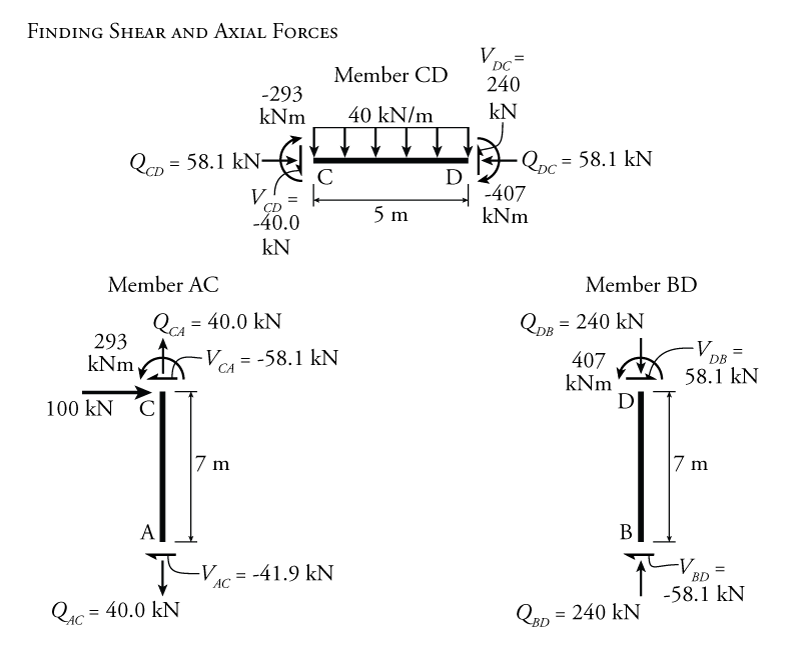
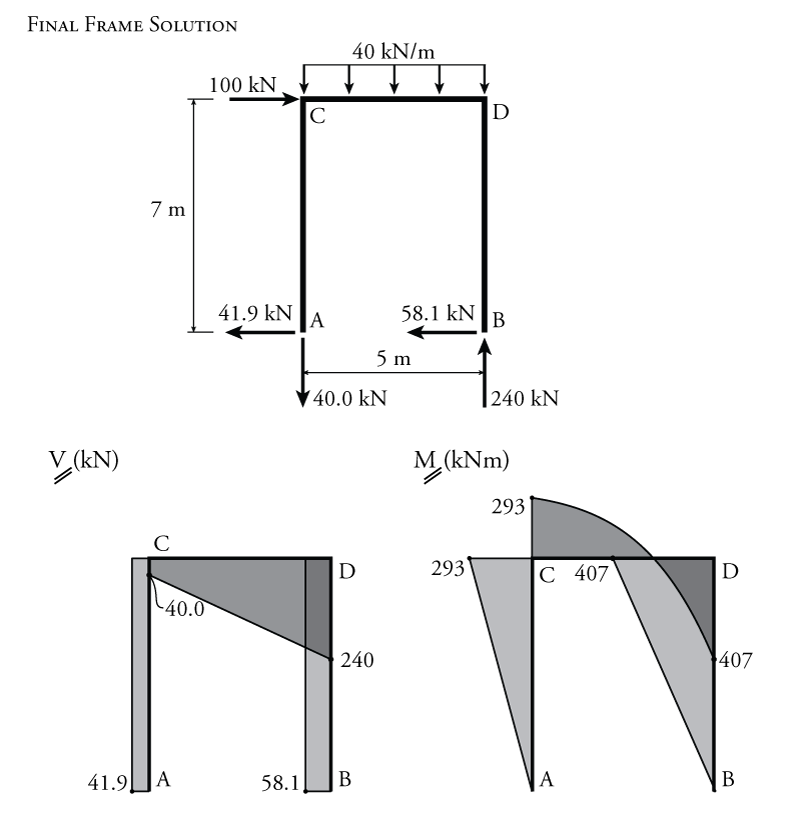
Using free body diagrams for each member, as shown in Figure 9.23, we can use the now-known end moments to find all the member end shears and axial forces. Then, we can use those free body diagrams to draw the final shear and moment diagrams as shown in Figure 9.24.
 Learn About Structures
Learn About Structures