>>When you're done reading this section, check your understanding with the interactive quiz at the bottom of the page.

​To calculate the reaction forces for a determinate 2D truss, you simply have to apply the three equilibrium equations to system as a whole to find the unknown forces. This process of finding reactions is identical to the process that was discussed in Section 1.2 for finding unknown forces using equilibrium. If there are more than three reaction components but the truss is still determinate due to an internal hinge (but is not unstable), then you would have to split the truss into separate free body diagrams to solve for all of the unknown reactions. We will encounter this problem in frame analysis.

Example

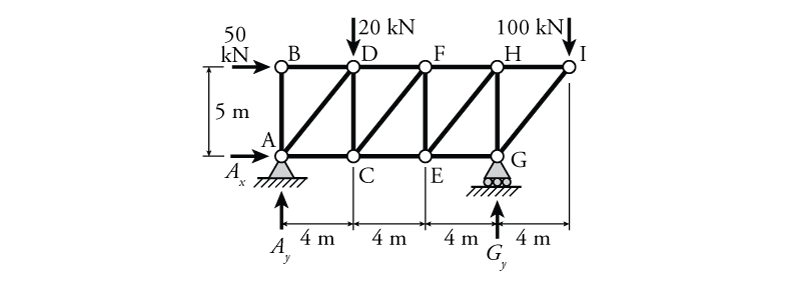
Find the reaction forces for the truss shown in Figure 3.4.

Figure 3.4: Reaction Calculation Example Problem

The unknown reaction forces $A_x$, $A_y$ and $G_y$ are shown in the figure. To find these unknown reactions, we need to apply the three equations of equilibrium to the entire truss. For the purposes of finding the reaction forces of determinate structures, we do not usually need to be interested in the `insides' of the structure (except in cases of more than three reaction force components). In this case, we can use the free body diagram of the entire truss to apply global equilibrium.

Let's start with moment equilibrium around point A. Since The unknown reactions $A_x$ and $A_y$ both push or pull directly on point A, neither of them create a moment around A. It is always a good idea to select a point for the moment equilibrium that eliminates as many of the unknown forces from the equation as possible. In this case, the only remaining unknown for the moment equilibrium around A will be $G_y$:

\begin{align*} \curvearrowleft \sum M_A &= 0 \\ - 50\mathrm{\,kN} ( 5\mathrm{\,m} ) &- 20\mathrm{\,kN} ( 4\mathrm{\,m} ) - 100\mathrm{\,kN} ( 16\mathrm{\,m} ) + G_y ( 12\mathrm{\,m} ) = 0 \\ G_y &= +160\mathrm{\,kN} \end{align*} \begin{equation*} \boxed{G_y = 160\mathrm{\,kN} \uparrow} \end{equation*}

The counter clock-wise rotation arrow $\curvearrowleft$ next to the equilibrium equation is to remind us that we consider CCW moments to be positive. In this equilibrium about point A, all of the external forces are clockwise, which, according to our sign convention described in Section 1.6, create negative moments. We have assumed in Figure 3.4 that the unknown reaction $G_y$ points upward. Since the resulting value for $G_y$ was positive, we know that this assumption was correct, and hence that the reaction $G_y$ points upward.

Next, consider vertical equilibrium. At the beginning of the problem, we had two vertical unknowns $A_y$ and $G_y$. Since we solved for $G_y$ using the moment equilibrium, the only vertical force unknown $A_y$ can easily be found using vertical equilibrium:

\begin{align*} \uparrow\sum F_y &= 0 \\ A_y - 20\mathrm{\,kN} - 100\mathrm{\,kN} + G_y &= 0 \\ A_y - 20\mathrm{\,kN} - 100\mathrm{\,kN} + 160\mathrm{\,kN} &= 0 \\ A_y &= -40\mathrm{\,kN} \end{align*} \begin{equation*} \boxed{A_y = 40\mathrm{\,kN} \downarrow} \end{equation*}

This time, the downwards arrow $\downarrow$ next to the equilibrium equation reminds us that we consider upwards forces to be positive. The negative result for $A_y$ indicates that $A_y$ points downwards (unlike the way it was assumed and shown in the figure).

For horizontal equilibrium, there is only one unknown, $A_x$:

\begin{align*} \rightarrow\sum F_x &= 0 \\ A_x + 50\mathrm{\,kN} &= 0 \\ A_x &= -50\mathrm{\,kN} \end{align*} \begin{equation*} \boxed{A_x = 50\mathrm{\,kN} \leftarrow} \end{equation*}

For the unknown reaction $A_x$, we originally assumed that it pointed to the right in the figure, therefore, since the result was negative we know it must actually pull to the left.