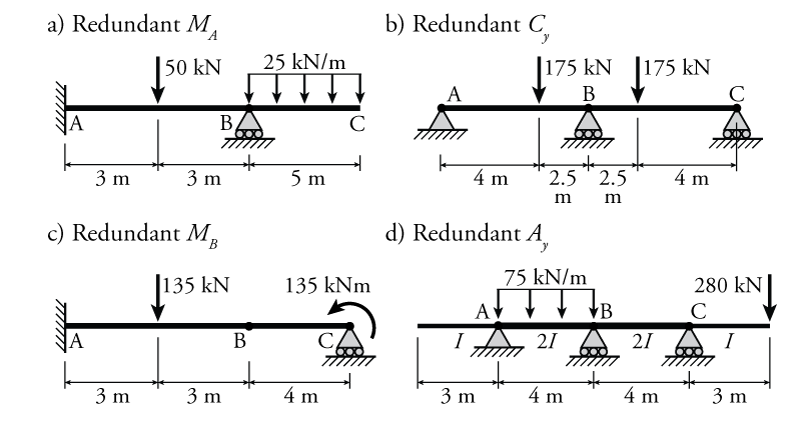
- For the beams shown below determine the reaction forces and draw the shear and moment diagrams using the force method. For each structure, use the specified redundant forces to do the force method analysis. All elements have the same $EI$ unless otherwise indicated.
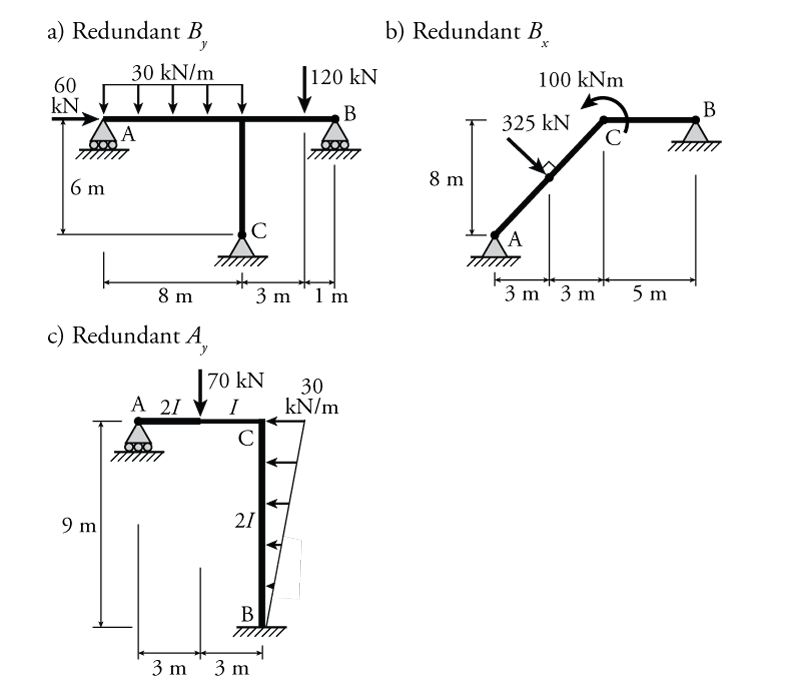
- For the frames shown below determine the reaction forces and draw the shear and moment diagrams using the force method. For each structure, use the specified redundant forces to do the force method analysis. All elements have the same $EI$ unless otherwise indicated.
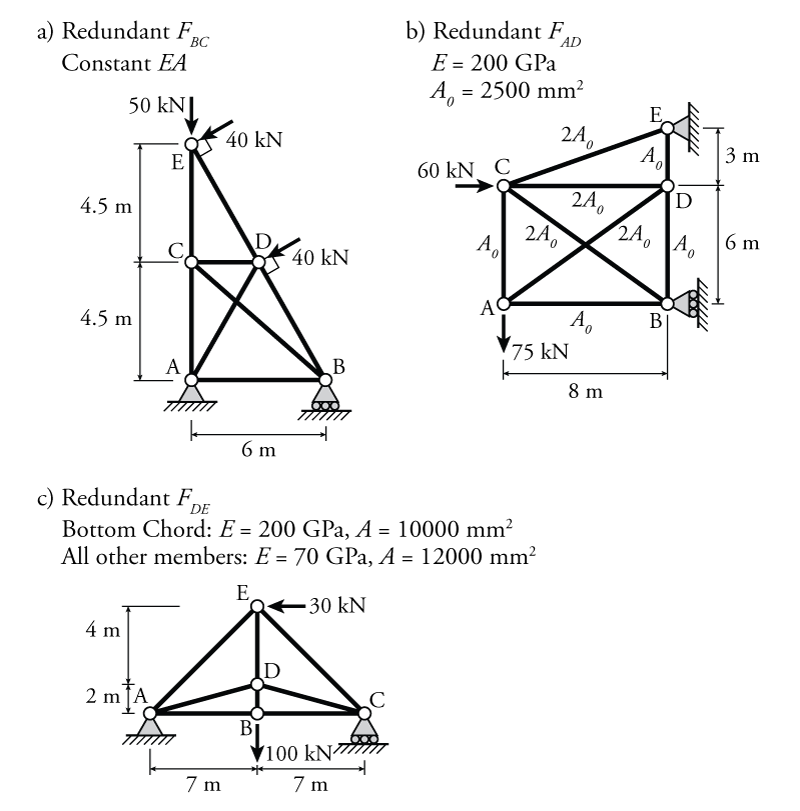
- For the trusses shown below determine the reaction forces and the internal axial forces in all members using the force method. For each structure, use the specified redundant forces to do the force method analysis. All elements have a constant $EA$ unless otherwise indicated.
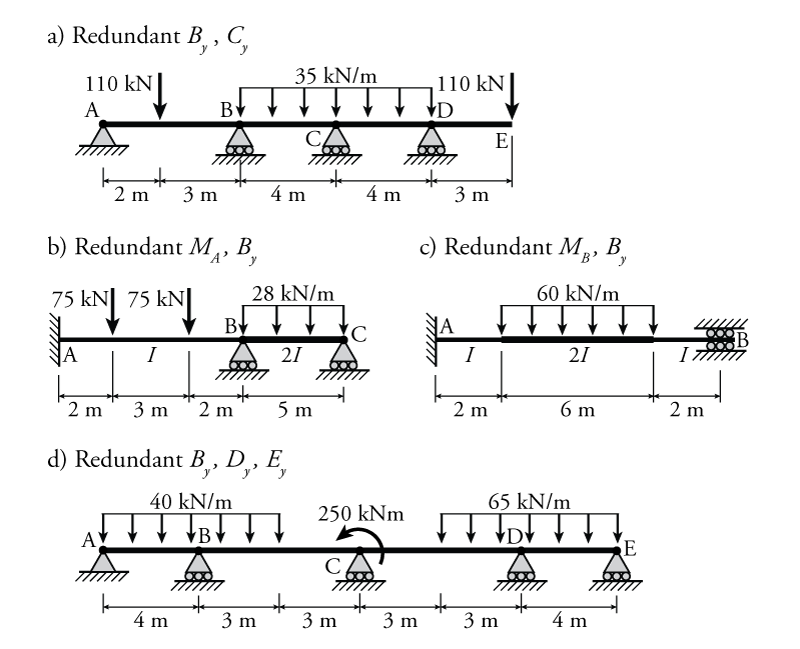
- For the beams shown below determine the reaction forces and draw the shear and moment diagrams using the force method. For each structure, use the specified redundant forces to do the force method analysis. All elements have the same $EI$ unless otherwise indicated.
- For the frames shown below determine the reaction forces and draw the shear and moment diagrams using the force method. For each structure, use the specified redundant forces to do the force method analysis. All elements have the same $EI$ unless otherwise indicated.
- Solve Problem 1(d) for the loading shown with the addition of a support settlement of $35\mathrm{\,mm}$ at support B. Assume $E = 200\mathrm{\,GPa}$ and $I=250\times 10^6\mathrm{\,mm^4}$.
- Solve Problem 1(b) for the loading shown with the addition of support settlements of $30\mathrm{\,mm}$ at support A, $10\mathrm{\,mm}$ at support B, and $45\mathrm{\,mm}$ at support C. Assume $E = 200\mathrm{\,GPa}$ and $I=\mathrm{\,400\times 10^6}{mm^4}$.
- Solve Problem 4(b) for the loading shown with the addition of support settlements of $15\mathrm{\,mm}$ at support B, and $10\mathrm{\,mm}$ at support C. Assume $E = 70\mathrm{\,GPa}$ and $I=500\times 10^6\mathrm{\,mm^4}$.
- Solve Problem 3(b) without any external loads, where members AB, AC and CE have undergone a temperature increase of $50\mathrm{\,^\circ C}$. Assume that $\alpha = 12\times 10^{-6}\mathrm{\,/ ^\circ C}$.
- Solve Problem 3(c) without any external loads, where member CE has undergone a temperature decrease of $-30\mathrm{\, ^\circ C}$ and member AE was fabricated $7\mathrm{\,mm}$ too long. Assume that $\alpha = 12\times 10^{-6}\mathrm{\,/ ^\circ C}$.
Resources for Structural Engineers and Engineering Students
 Learn About Structures
Learn About Structures