Learn About StructuresThe moment distribution method is the third method that we will learn for the analysis of indeterminate structures. Recall that the force method was good for structure with a small number of degrees of indeterminacy, regardless of how many degrees-of-freedom the system has. In contrast to that, the slope-deflection method was good for structures with a small number of degrees-of-freedom, regardless of how many degrees of indeterminacy the system has. The moment distribution method is an iterative method that gets around the problem of too many degrees of indeterminacy or too many degrees of freedom. Using moment distribution, we can analyse highly indeterminate structures with many degrees of freedom by hand.
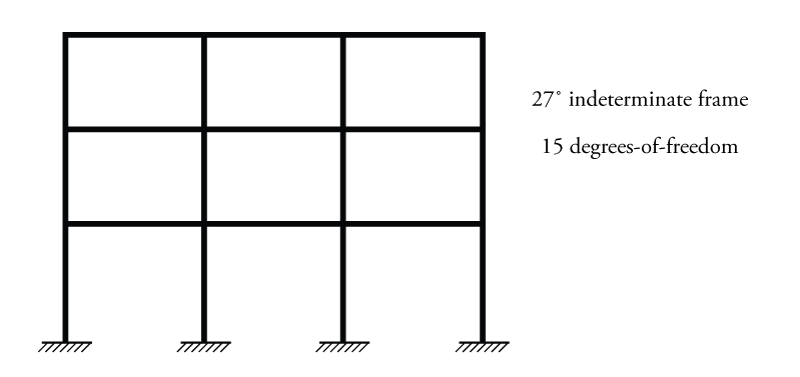
For example, the structure shown in Figure 10.1 is typical for a concrete building frame. The structure has rigid connections between all of the members, and this results in 27 degrees of static indeterminacy and 15 degrees of freedom. This system would clearly be all but impossible to analyse using the force method or the slope-deflection method. Prior to the development of the moment distribution method in 1932, there was simply no practical way to analyse such a system.
The moment distribution method is also called the Hardy Cross method after its inventor, an engineering professor named Hardy Cross. Cross published this method in a single, concise ten page paper in September of 1932.(Cross, H. (1949) Analysis of Continuous Frames by Distributing Fixed-End Moments. Transactions of the American Society of Civil Engineers, Vol. 96, No. 1, January 1932, pp. 1-10). The publication of this method immediately revolutionized the practice of structural engineering because it suddenly made the precise analysis of structures such as the one in Figure 10.1 possible.
The moment distribution method is an exact method that relies on a set of successive better approximations to determine the bending moments for beams and frames.