There is an alternate to the equilibrium method for constructing influence lines. This method is based on the Müller-Breslau Principle, and may also be called qualitative influence lines. This method allows us to draw influence lines faster than if we use the equilibrium calculations described in the previous section. In fact, it is likely that if we wanted to construct a shear or moment influence line using this method, then we would not have to find the reaction influence lines for the structure first.
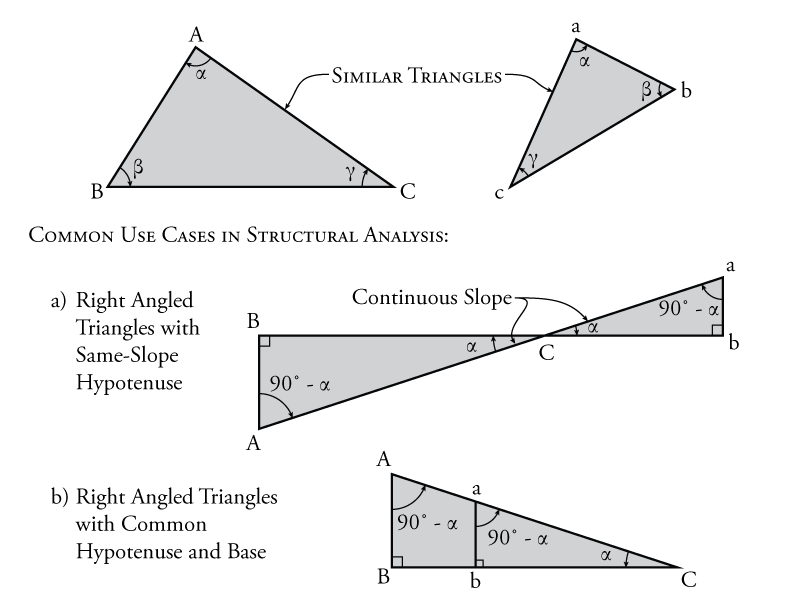
Similar Triangles
Before explaining the Müller-Breslau Principle, it is useful to review the concept of similar triangles, which you will likely have studied previously at the high-school level. The concept of similar triangles is illustrated in Figure 6.6.
Two triangles are considered similar triangles if they have three identical internal angles, as shown in Figure 6.6 (where the three angles are labelled $\alpha$, $\beta$ and $\gamma$). It doesn't matter if one triangle has a larger area than the other, which way the triangles are rotated relative to each other, or whether one is the mirror image of the other (i.e. if it is flipped relative to the other like the two triangles at the top of Figure 6.6).
If you do not know the full geometry of two triangles (the angles and the lengths of the sides), you can determine that two triangles are similar in three ways:
- AAA - All of the angles are the same between the two triangles (or really, AA because for triangles, if two angles are the same, the last one must also be the same since they all add up to 180)
- SSS - All of the sides are in the same proportion between the two triangles
- SAS - Two of the sides are in the same proportion between the two triangles and they share one identical angle
For structural analysis, and influence lines in particular, some of the more common situations where similar triangles are useful are shown in the lower part of Figure 6.6.
The first situation is when you have right angled triangles that are joined at the nose and share a common angle at that location (situation (a) in Figure 6.6). This situation is common if the hypotenuse of the triangles is the influence line that has a continuous and constant slope, but crosses the horizontal axis. These two triangle are AAA similar because they share three equal angles ($\alpha$, the right angles, and the last angle which must equal ${90^\circ} - \alpha$). For this situation, you may know the heights of the triangles and want to find the location of point C, which you can find by taking advantage of the fact that the sides of the triangles will be in proportion:
\begin{align*} \frac{BC}{bC} &= \frac{AB}{ab} \\ BC &= \frac{AB \times bC}{ab} \end{align*}
Knowing the total length of the bases of both triangles together:
\begin{align*} \frac{BC}{Bb} &= \frac{AB}{AB+ab} \\ BC &= \frac{AB \times Bb}{AB+ab} \end{align*}
Or, you may know the height and base of one triangle and the base of the other and want to find the height of the other triangle:
\begin{align*} \frac{AB}{ab} &= \frac{BC}{bC} \\ AB &= \frac{BC \times ab}{bC} \end{align*}
The second common situation shown in Figure 6.6 is that you have the dimensions of a bigger right-angled triangle and you want to find the height of the hypotenuse line at a different location $a$ along the length (situation (b) in the figure). This can be found by imagining a smaller similar right-angled triangle that shares the same hypotenuse but that has a shorter base length as shown. If we know the height of the larger triangle and want to find the height of the smaller one:
\begin{align*} \frac{ab}{AB} &= \frac{bC}{BC} \\ ab &= \frac{bC \times AB}{BC} \end{align*}
Müller-Breslau for Horizontal and Vertical Reactions
The basis of the Müller-Breslau Principle is that we can find the influence line for a determinate beam by:
- Removing the restraint caused by the parameter that we want to find the influence line for; then,
- Displace or rotate the resulting structure by one unit.
If the restraint that is removed is an internal shear or a vertical or horizontal support, then the second step is to displace the structure at that same location. If the restraint that is removed is an internal moment or a rotational restraint, then the second step is to rotate the structure at that same location. If the structure is determinate, then removing the support will cause the structure to become unstable. Therefore, it will be able to move freely, without any stiffness. The trick to the Müller-Breslau Principle is that you must figure out how the rest of the structure will move after applying the unit displacement or rotation. Since the determinate structure has lost its stiffness it also means that none of the member will bend when the unit displacement or rotation is applied. All the pieces will remain straight.
So, for a vertical or horizontal reaction component, the influence line for that reaction is constructed by removing the reaction component and then displacing the structure by 1.0 in the location of the reaction component and in the same direction as that component. This process is illustrated in Figure 6.7.
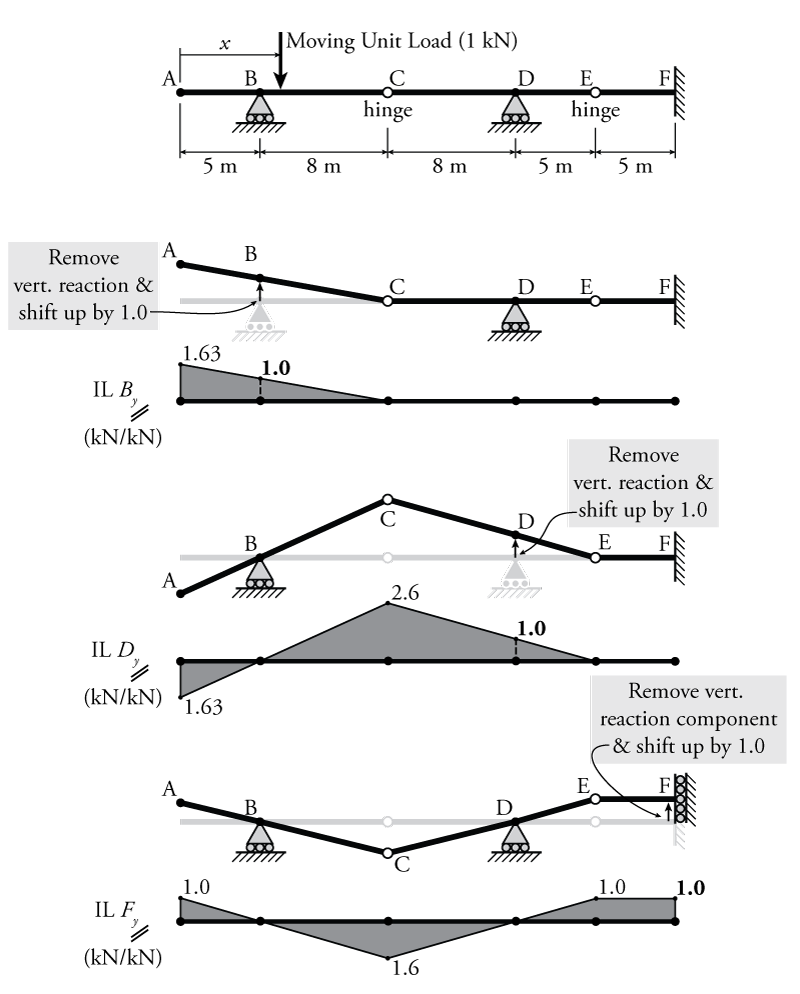
In Figure 6.7, a full example structure is shown at the top. This example structure has two roller supports, one at point B and one at point D, and a fixed support at the right end at point F. Two internal hinges, at points C and E, provide two equations of condition, making the beam determinate. To find influence lines for this beam, we will consider that there is a moving unit load that travels from the left side at point A ($x = 0$) to the right side at point F ($x=31$).
To find the influence line for the vertical reaction at point B, the process is shown in Figure 6.7. The roller only provides a vertical reaction, so we remove the roller support (making the structure unstable in the process), and move point B upwards by 1.0 as shown in the figure. Since the beam is now unstable, it is free to move in this way, rotating at the hinge at point C. The resulting shape of the structure now represents the influence line for the vertical reaction at point B (IL $B_y$) as shown in the figure. The value of the influence line at B is 1.0 (the amount that we moved point B upwards), as we would expect, since when the moving unit load is directly above point B, all of the load will go straight into the vertical support at B. The value of the influence line at point A may be found to be 1.63 using similar triangles:
\begin{align*} \text{IL }B_y ( \text{at }x = 0) = \frac{8 + 5}{8} (1.0) = 1.63 \end{align*}
Recall that this means that when there is a unit point load at point A, then the vertical reaction at point B ($B_y$) will equal 1.63. This result may be double-checked using equilibrium.
Likewise, to find the influence line of the vertical reaction at D (IL $D_y$), we must remove the vertical reaction at D and shift the now unstable structure upwards by 1.0 as shown in Figure 6.7. Obviously, this necessitates being able to visualize how the structure will move once it is unstable. Since the structure becomes unstable, all of the members will remain straight and we must assume that all members remain rigid. So for this influence line vertical reaction at D, when we remove the vertical reaction, the structure must pivot at the hinges at points C and E, but the structure remains held down at point B by the other roller support. The section of the beam between E and F must remain horizontal and rigid because it is fixed at F. The resulting influence diagram for this beam mirrors the shape of the deformed unstable structure and is shown in the figure (IL $D_y$). The value of the influence line at point D is equal to 1.0, since the structure was moved upwards by 1.0 at point D when the vertical reaction was removed. The remaining values on the influence line diagram may be found using similar triangles. For the value at C:
\begin{align*} \text{IL }D_y (\text{at } x = 13) = \frac{8 + 5}{5} (1.0) = 2.6 \end{align*}
Likewise, using this value, we can find the value of the influence line at A:
\begin{align*} \text{IL }D_y (\text{at } x = 0) = \frac{5}{8} (2.6) = 1.63 \end{align*}
The last influence line shown in Figure 6.7 is for the vertical reaction at point F. This is a bit more complex than for the previous reactions because we cannot completely remove the support (like we did for the rollers), but must only remove the component of the fixed support that resists vertical forces. When we do this, we are left with a complex support at point F that may resist moment, but not vertical forces (see Section 1.5). When point F is shifted upwards (which is possible now that the vertical reaction component has been removed), the whole beam section EF shifts upwards too but remains horizontal because it is not allowed to bend and is still fixed for rotation at point F by the complex support condition there. The rest of the beam deforms as shown in the figure since this is the only way that the beam pieces can move while still remaining held down and in position at the remaining roller supports at points B and D. The resulting influence diagram for the vertical reaction component at point F (IL $F_y$) is shown at the bottom of Figure 6.7. The section of the beam between E and F have a value of 1.0 because that is the distance that the unstable beam was shifted upwards when the vertical reaction at point F was removed. The other points on the influence diagram may be found using similar triangles and is left as an exercise.
Müller-Breslau for Moment Reactions
To find the influence line for a moment reaction, the process is very similar to that for the vertical reaction forces described above except that the moment restraint at the reaction location is removed (instead of the vertical reaction restraint). This process is illustrated in Figure 6.8. The structure shown here is the same structure that was used for the previous Figure 6.7.
To find the influence line for the moment reaction at point F (IL $M_F$), the rotational reaction component is removed from the fixed support. This again causes the determinate structure to become unstable, leaving a pin at point F. Once the rotational support is removed, the beam is rotated at point F by $1.0\mathrm{\,rad}$. This is a counter-clockwise rotation because we are considering counter-clockwise rotations and moments to be positive. Again, all of the beam segments must remain straight and rigid as they move. This results in the displaced structure shown in the middle of Figure 6.8, with rotations in the internal hinges at points C and E, and with the beam being held down at the roller and pin supports at points B, D and F. This displaced shape results in the equivalent influence line shown at the bottom of the figure (IL $M_F$), where the slope at the right side at point F is 1.0. Using this slope, we can directly find the value of the influence line at point E:
\begin{align*} \text{slope} &= \frac{\text{rise}}{\text{run}} \\ \text{IL }M_F (\text{at } x = 26) &= \text{slope} \times \text{run} \\ &= 1.0 (5) = 5.0 \end{align*}
This value means that when a point unit load ($1\mathrm{\,kN}$) is placed at point E, the moment reaction at point F $M_F = 5\mathrm{\,kNm}$. The remainder of the values on the influence line may be found using similar triangles.
Müller-Breslau for Internal Shear Forces
The influence lines for vertical and rotational reactions described above are quite conceptually simple to create and use; however, influence lines for internal beam moments and shears may be a bit more conceptually difficult. Once you get the hang of them though, they can save a lot of time compared to using equilibrium to find them as described in previous Section 6.2.
To find the influence line for internal shear at a point, you must break the beam in shear at that point and displace the broken ends relative to each other (so one will go up and the other end will go down); When the beam is displaced, the slope of the beam on either side of the break must be the same because we have only removed the beam's ability to take shear at the break, not internal moment. This restriction on the slope allows the determination of the relative movement of either side of the beam break using similar triangles.
Examples of internal shear force influence line construction are shown in Figure 6.9 (this is for the same beam as before). To find the influence line for the shear in the beam at a point $2\mathrm{\,m}$ to the right of point D (shown as point D') we must break the beam in shear at point D' and displace the broken ends. This is shown in Figure 6.9 (second from the top) According to our sign conventions (see Section 1.6), the convention for positive shear is left side of the beam up and right side of the beam down. So, for the section on the left of the break (DD'), since the break is on the right side of this section beam, it will move downwards. Likewise, the other side of the break (D'E) will move upwards. The total relative displacement of the two ends should be 1.0. To find the value of the displacement at each displaced end, we can use similar triangles.
These triangles may be seen on the influence line for shear at point D' in Figure 6.9. The two trianges are between points D and D' and between points D' and E (the two triangles that are labelled with heights 0.4 and 0.6). Since the slope must be constant on each side of the break, the two angles at the toes of the triangles much be the same. Since they are also both right-angled triangles, all three angles must be the same between the two and they are similar triangles. Therefore, the height of the shorter triangle must be:
\begin{align*} \text{IL }B_D' (\text{just left of } x = 23) &= - \frac{2}{5}(1.0) = -0.4 \end{align*}
Likewise:
\begin{align*} \text{IL }B_D' (\text{just right of } x = 23) &= \frac{3}{5}(1.0) = 0.6 \end{align*}
Knowing these points, the rest of the influence line may be determined using similar triangles. Notice that the displaced shape of the unstable structure is zero for the beam segment between E and F since that segment is restrained by the fixed end at F. This means that if the moving unit load is located between E and F, then there will be no shear at point D'.
A second example shear influence line is shown in Figure 6.9 for the shear at point C' which is $6\mathrm{\,m}$ to the right of point C. The beam is broken in shear at point C' and again the left side (CC') is displaced downwards and the right side (C'D) would be displaced upwards; however, in this case, the right side of the break cannot move because of the fixed end at F. That fixed end means that point E cannot move, and since segment DE is also restrained by the roller at D, the broken end at point C' (right) also cannot move. The right side of the break must also therefore stay horizontal. So, since the slopes on either side of the break must be the same, segment CC' must also be horizontal. The left side takes the full value of the displacement (1.0) since the right side is restrained.
The resulting influence line is shown at the bottom of Figure 6.9 (IL $V_{C'}$). The value of the influence line between C and C' is equal to 1.0 because that is how much that segment of the beam is shifted down when the beam is broken for shear at point C'. The remaining points on the influence line may be found using similar triangles. The entire right side of the influence line to the right of point C' is zero. This means that any load that is applied to the beam to the right of point C' does not cause any shear at point C'.
Müller-Breslau for Internal Moments
Similar to the shear, an internal moment influence line for a certain point is constructed by breaking the beam for moment at that point (while retaining the beam's ability to take shear). This is easier to conceptualize than the shear case because adding an internal hinge to the beam at that point easily releases the internal moment restraint. Therefore, to find the influence line for an internal moment at a point, add a hinge to the beam at that point and then rotate the beam at that point by a total of $1.0\mathrm{\,rad}$.
Two examples of internal moment influence lines are shown in Figure 6.10. These are for the same points C' and D' as for the shear force influence diagrams in the previous section.
For the moment point D', a hinge is added at D' as shown in Figure 6.10. Then both sides of the hinge are rotated in the positive sense for internal moment as discussed in Section 1.6, clockwise on the left end of a beam (right side of the hinge), and counter-clockwise on the right end of a beam (left side of the hinge). The total amount of rotation at the hinge should be equal to $1.0\mathrm{\,rad}$ as shown in the figure.
The resulting influence line is shown in Figure 6.10 (IL $M_{D'}$). The section EF is again restrained by the fixed end and does not move. To find the total value of the influence line at point D', you need to know the angles of the triangles between D and D' and between D' and E. The total angle is 1.0, and this total amount is split between the two triangles in inverse proportion to the base length of the triangles. For the left triangle (DD'), the slope is $(1.0) \frac{3}{5} = 0.6$ and for the right triangle, it is $(1.0) \frac{2}{5} = 0.4$. This means that the height of the triangle can be calculated as $0.6(2\mathrm{\,m})=1.2$ or $0.4(3\mathrm{\,m})=1.2$.
Of course, there is an alternate way to easily find the value of the influence line for the moment at D'. We could simply start with the original structure, put a unit point load at point D' and then use equilibrium to find the moment at that point. This method will always work, so it is possible to construct an influence line by first using Müller Breslau to find the shape, then using equilibrium to find the value of the influence diagram at a single point. After that similar triangles may be used to find the rest of the points on the influence diagram.
A second example of an internal moment influence diagram is also shown in Figure 6.10 for the moment at point C' (IL $M_{C'}$). For this case, a hinge is added to the structure at point C', causing the structure to become unstable. Similarly to the shear influence line case, the right side of the hinge to the right of C' cannot rotate due to the connection through the hinge at E to the fixed end at F. Therefore, for this case all of the rotation happens on the left side of the hinge. This means that segment CC' rotates by a full $1.0\mathrm{\,rad}$, making it easy to find the value of the influence line at point C as slope multiplied by run which equals 6.0. The other values on the influence line may be found using similar triangles.
 Learn About Structures
Learn About Structures