>>When you're done reading this section, check your understanding with the interactive quiz at the bottom of the page.

Stable/Unstable

A stable structure is one that will not collapse when disturbed. Stability is the capability for a structure to recover equilibrium. In general, there are many ways that a structure may become unstable, including buckling of compression members, yielding/rupture of members, or nonlinear geometric effects (like so-called P-Delta effects); however, in linear structural analysis, our main concern is instability caused by insufficient reaction points or poor layout of structural members.

Internally Stable

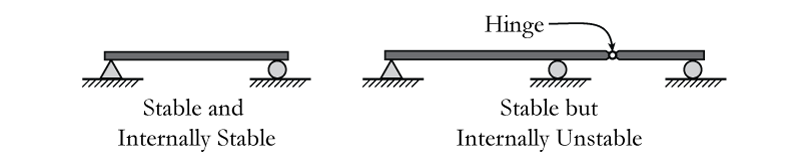
An internally stable structure is one that would maintain its shape if all the reaction supports were removed. A structure that is internally unstable may still be generally stable if it has sufficient external support reactions. Examples of internal stability and internal instability are shown in Figure 2.1.

Figure 2.1: Internal Stability

External Determinacy

In an externally statically determinate structure, all of the external reaction force components may be calculated using only static equilibrium (i.e. using the three equilibrium equations in 2D). A structure for which the external reactions component forces cannot be calculated using only equilibrium is called externally statically indeterminate.

Internal Determinacy

In an internally statically determinate structure, all of the external reaction component forces and internal forces may be calculated using only static equilibrium. A structure for which the internal forces cannot be calculated using only equilibrium is internally staticallyindeterminate.+Typically if one talks about `determinacy' (without specifying internal or external), then it is internal determinacy that is intended.

Redundant Forces

​Indeterminate structures have more unknown forces than you can solve using the three equilibrium equations alone (or six equilibrium equations in 3D). These extra unknown forces are called redundant forces or redundants.

Degree of Indeterminacy

The degree of indeterminacy for a structure is equal to the number of redundant forces. An indeterminate structure with 2 redundants may be said to be statically indeterminate to the second degree or "$2^\circ$ S.I."