An unstable structure generally cannot be analysed. Therefore, it is useful to know if a structure is stable or unstable before you conduct a structural analysis. There are four main ways that a structure may be geometrically unstable. These apply only to linear geometric stability and not to instability caused by buckling, member yielding or nonlinear geometry (which are outside the scope of this course).
- There are not enough reactions: This will generally be clear from an application of the determinacy equations \eqref{eq:SI-Unstable} to \eqref{eq:SI-Indet} (or \eqref{eq:Truss-Unstable} to \eqref{eq:Truss-Indet} for trusses). \begin{align} \text{Statically unstable internally: } 3m + r &< 3j + e_c \label{eq:SI-Unstable} \tag{1} \\ \text{Statically determinate internally: } 3m + r &= 3j + e_c \label{eq:SI-Det} \tag{2} \\ \text{Statically indeterminate internally: } 3m + r &> 3j + e_c \label{eq:SI-Indet} \tag{3} \end{align} \begin{align} \text{Statically unstable internally (truss): } m + r &< 2j \label{eq:Truss-Unstable} \tag{4} \\ \text{Statically determinate internally (truss): } m + r &= 2j \label{eq:Truss-Det} \tag{5} \\ \text{Statically indeterminate internally (truss): } m + r &> 2j \label{eq:Truss-Indet} \tag{6} \end{align}
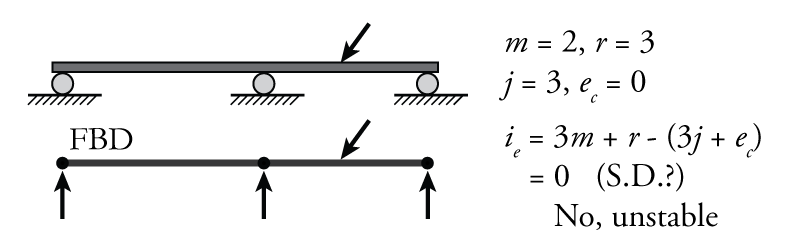
- The reactions are parallel: All of the reaction components point in the same direction. An example of such a situation is shown in Figure 2.5. In this example, the horizontal equilibrium $\sum {F_x} = 0$ cannot be solved. Since there are no reaction forces in the x-direction, there will be a net horizontal force on the system with no resistance.
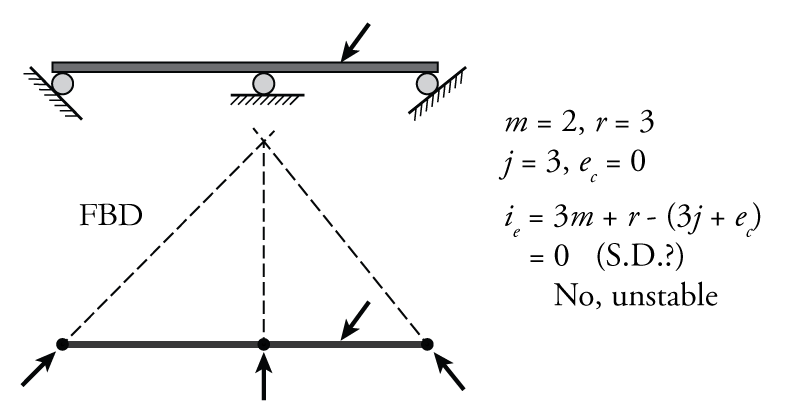
- The reactions are concurrent: All of the reaction components meet at a point. This instability is more subtle and may be difficult to spot. An example of such a situation is shown in Figure 2.6. Effectively, when the reactions are concurrent, the system is free to rotate as a rigid body around the point where the reaction components meet.
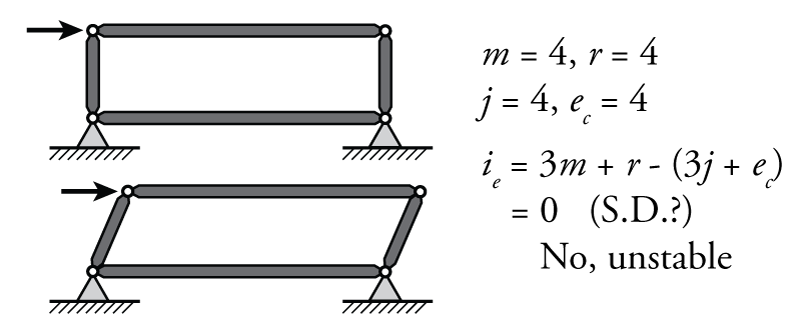
- There is an internal collapse mechanism: This scenario includes any situation in which there is an internal mechanism in the system that will cause it to deform between the supports. In some such situations, this will be clear from the use of the determinacy equations, but in others, it may not be. In all such cases, though, the instability will become clear during the structural analysis because it will be impossible to solve for all of the internal forces. An example internal collapse mechanism is shown in Figure 2.7.
Examples
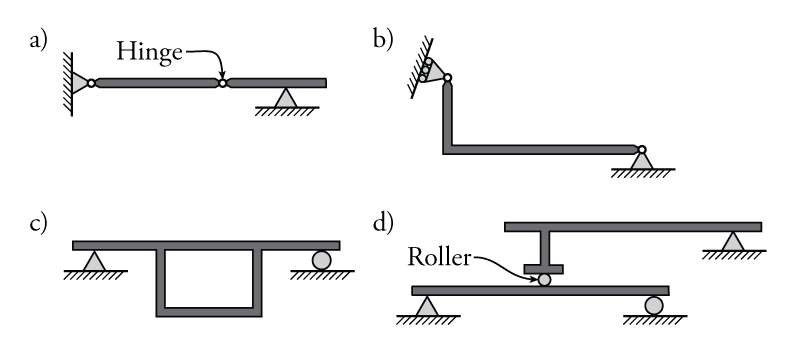
Determine whether the structures shown in Figure 2.8 are externally determinate, internally determinate, externally indeterminate, internally indeterminate or unstable. If a structure is indeterminate, determine how many degrees of indeterminacy it has.
-
- External Determinacy: \begin{align*} i_e &= r - (3+ e_c) \\ r &= 4, \; e_c = 1 \end{align*} (The hinge on the left at the pin does not provide any additional equations of condition). Therefore, $i_e = 0$. Then, is this structure statically determinate? No, it is unstable because if we take a free-body diagram of the left side of the beam, and take a sum of moments about the center hinge, the sum of moments will be non-zero due to the vertical reaction at the left pin (but we know that it has to be zero due to the existence of the pin).
- Internal Determinacy: \begin{align*} i_e &= (3m+r) - (3j+e_c) \\ m &= 2, \; r = 4, \; j = 3, \; e_c = 1 \end{align*} (Again, the hinge on the left at the pin does not provide any additional equations of condition). Therefore, \begin{align*} 3m+r = 10, \; 3j+e_c = 10, \text{ and } i_e = 0 \end{align*} Then, is this structure statically determinate? No, it is unstable due to the same reason above.
-
- External Determinacy: \begin{align*} r = 3, \; e_c = 0 \end{align*} Therefore, $i_e = 0$. Then is this structure statically determinate? No, because the reactions are concurrent through the pin on the right.
- Internal Determinacy: \begin{align*} m = 2, \; r = 3, \; j = 3, \; e_c = 0 \end{align*} Therefore, \begin{align*} 3m+r = 9 \text{ and } 3j+e_c = 9 \end{align*} so the structure appears internally determinate, but it is still unstable due to the concurrent reactions.
-
- External Determinacy: \begin{align*} r = 3, \; e_c = 0 \end{align*} Therefore, $i_e = 0$. Since there are no sources of instability, this structure is externally statically determinate.
- Internal Determinacy: \begin{align*} m = 6, \; r = 3, \; j = 6, \; e_c = 0 \end{align*} Therefore, \begin{align*} 3m+r = 21 \text{ and } 3j+e_c = 18 \end{align*} so this structure is internally statically indeterminate to three degrees (or "3$^\circ$ S.I.").
-
- External Determinacy: \begin{align*} r = 5, \; e_c = 2 \end{align*} Therefore, $i_e = 0$. Since there are no sources of instability, this structure is externally statically determinate.
- Internal Determinacy: \begin{align*} m = 5, \; r = 5, \; j = 6, \; e_c = 2 \end{align*} Therefore, \begin{align*} 3m+r = 20 \text{ and } 3j+e_c = 20 \end{align*} so this structure is internally statically determinate (or "S.D.").
Book traversal links for 2.6 Stability
Interactive Quiz
 Learn About Structures
Learn About Structures