>>When you're done reading this section, check your understanding with the interactive quiz at the bottom of the page.

If a structure is internally determinate, then all of the reactions and internal forces may be calculated using equilibrium alone. Internal determinacy is generally much more important than external determinacy in structural analysis. To calculate internal determinacy, the following equations are used:

\begin{align} \tag{1} \text{Statically unstable internally: } 3m + r &< 3j + e_c \label{eq:SI-Unstable} \\ \tag{2} \text{Statically determinate internally: } 3m + r &= 3j + e_c \label{eq:SI-Det} \\ \tag{3} \text{Statically indeterminate internally: } 3m + r &> 3j + e_c \label{eq:SI-Indet} \end{align}

where $m$ is the total number of members in the structure, $r$ is the number of reaction components, $j$ is the total number of joints in the structure, and $e_c$ is the number of equations of condition. The meaning of $r$ and $e_c$ are the same as for External Determinacy described in Section 2.3. The definition of members and joints will be discussed in the next section.

The degree of indeterminacy $i_e$ for internal indeterminacy is given by the following equation:

\begin{equation} \tag{4} \boxed{i_e = 3m + r - (3j + e_c) } \label{eq:deg-indet} \end{equation}

As it was for external determinacy, if this equation results in $i_e= 0$, the structure is determinate; if it results in $i_e < 0$, then the structure is unstable. Otherwise, $i_e$ is the degree of indeterminacy (i.e. how many extra redundant forces there are). Note that even if a structure seems to be stable according to the equations above, instability can be caused by additional mechanisms that will be discussed in Section 2.6.

Members and Joints

There is no specific way that a structure must be split into members and joints for the purposes of the determinacy analysis. Any division of the structure is okay as long as the members and joints are consistent with each other; however, joints should be placed at least at the following locations:

• Free ends
• Reactions
• Intersections of three or more elements

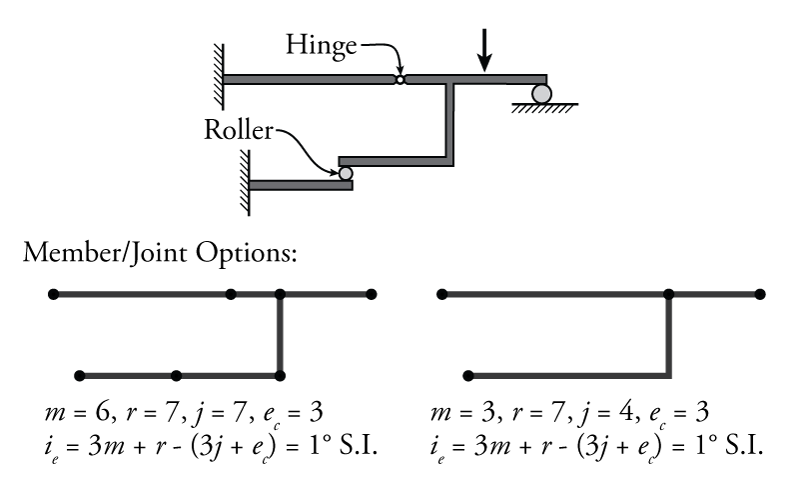
For an example of how to calculate the numbers of members and joints, see Figure 2.4.

Figure 2.4: Determination of the Number of Members and Joints