The moment area theorems provide a way to find slopes and deflections without having to go through a full process of integration as described in the previous section. They still rely on the Bernoulli-Euler beam theory assumptions (plane sections remain plane and small angles).
There are two moment area theorems, one that relates to the slope of the beam and one that relates to the deflections. It is important to understand that both theorems only provide information about one location on a beam relative to another location on the beam. They are quite powerful once you know how to use them properly.
First Moment Area Theorem
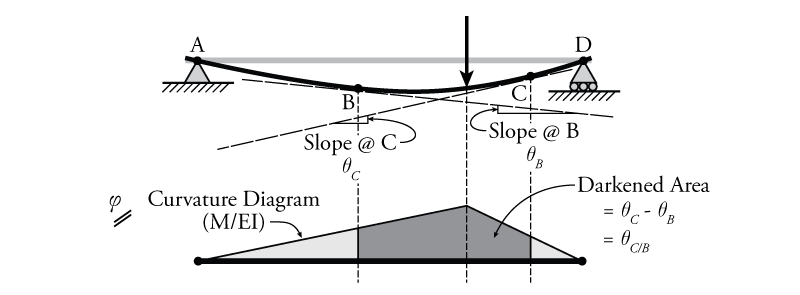
The first moment area theorem is that the change in the slope of a beam between two points is equal to the area under the curvature diagram between those two points. Recall that the curvature is just equal to $M/EI$, so the curvature diagram often looks similar to the moment diagram; however, be careful, because it is possible for $EI$ to change along the length of a beam, which may cause 'steps' in the curvature diagram, which won't be present in the moment diagram.
The first moment area theorem is illustrated in Figure 5.4. The sample structure in the figure is a simply-supported beam with a point load. This support condition and loading on the beam results in a triangle-shaped moment diagram. To find the curvature diagram, you would have to divide the moment diagram by $EI$ at every point along the beam. If the $EI$ of the beam is the same all the way along, this results in a simple scaling of the moment diagram and the curvature diagram so the curvature diagram would also have a triangular shape as shown in the figure (but with different magnitude).
Once we have a curvature diagram, we can use the moment area theorems. The first moment area theorem, described above, relates the slope (rotation) at one point along a beam to the slope at another point on the beam. The slopes at two points along the sample beam (points B and C) are shown in Figure 5.4. The change in slope between points B and C is equal to the area under the curvature diagram between points B and C as shown (which is the same thing as the integral of the curvature). This change in slope is referred to as $\theta_{C/B}$:
\begin{align} \tag{1} \theta_{C/B} = \theta_C - \theta_B \end{align} \begin{equation} \tag{2} \boxed{\theta_{C/B} = \int_B^C \frac{M(x)}{E(x)I(x)} \, dx} \end{equation}
Second Moment Area Theorem
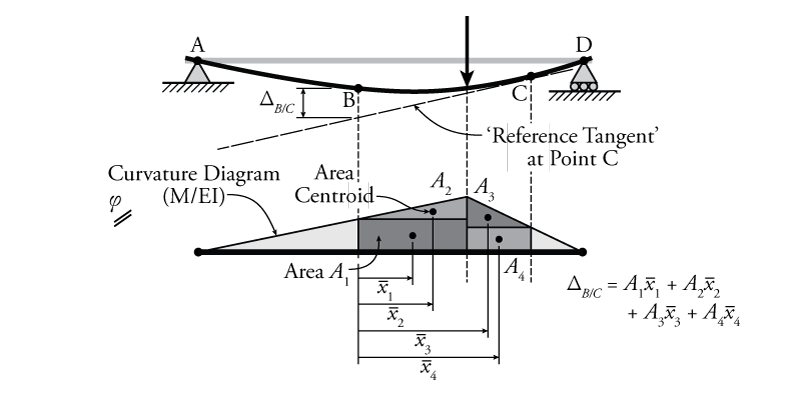
The second moment area theorem is that the vertical distance between (a) a reference tangent line that is tangent to the slope at one point on the beam and (b) the deflected shape of the beam at another point, is equal to the moment of the area under the curvature diagram between the two points with the moments of the areas calculated relative to the point on the deflected shape (b).
The second moment area theorem is illustrated in Figure 5.5. The same sample structure is used for this illustration as for the first moment area theorem in the previous sections, so it has the same curvature diagram.
The second moment area theorem relates the tangent line at one point on a beam (our reference tangent) to the deflection of another part of the beam, as shown in Figure 5.5; however, it is important to realize that this can give us only the distance between the reference tangent line and the deflected shape ($\Delta_{B/C}$ in the figure), it cannot directly give us the deflection of the beam relative to the initial undeformed shape (which is usually the parameter that we are most interested in). We can use the second moment area theorem to find total deflection relative to the undeformed position, but it is a multi-step process, as we will learn in the next section.
For the second moment area theorem itself, that relative distance (between a reference tangent at one point and the deflected shape at another point) is found by taking the moment of the area under the curvature diagram between the two points. This is actually a similar process to the process required to find the centroid of a cross-section. If the area under the curvature diagram is a complex shape then we can split it up into smaller areas with simple shapes ($A_1$ to $A_4$ as shown in Figure 5.5) and find the sum of the moments of the areas for each of them. A moment of an area is simply the area of the shape ($A$) multiplied by the distance to the centroid ($\bar{x}$) as shown in the figure. For the second moment area theorem, that distance is always measured from the deflected shape point (B in the figure). In the figure, this results in a distance between the reference tangent and the deflected shape of:
\begin{align} \tag{3} \Delta_{B/C} = A_1 \bar{x}_1 + A_2 \bar{x}_2 + A_3 \bar{x}_3 + A_4 \bar{x}_4 \end{align} \begin{equation} \tag{4} \boxed{\Delta_{B/C} = \int_B^C \frac{M(x)}{E(x)I(x)} \bar{x} \, dx } \end{equation}
Using the Moment Area Theorems
This section will outline two common scenarios that are often encountered for which the moment area theorems can be very useful.
Slope and Deflection are both Zero at One Point
If we know the slope and deflection at a single point in a beam are both zero (at the same point), as shown in Figure 5.6, then we can easily find the slope or deflection anywhere else on the beam in one step. This situation happens most commonly if our beam has a fixed end, like the cantilevered beam shown in the figure.
With reference to Figure 5.6 part (a), we know that the slope at point A ($\theta_A$) is zero (because the fixed end does not permit rotation). Since we know the slope at point A, we can find the slope anywhere else on the beam using the first moment area theorem. For example, if we want to find the slope at point B, the change in the slope between points A and B is equal to the area under the curvature diagram between A and B as shown by the darkened portion of the curvature diagram in the figure, as previously described in First Moment Area Theorem:
\begin{equation*} \theta_{B/A} = \int_A^B \frac{M(x)}{EI} \, dx \end{equation*}
In this case, this change in slope ($\theta_{B/A}$) is equal to the area of the shaded trapezoid (or can be calculated as the area of a rectangle plus the area of a triangle as shown in part (b) of the figure). Knowing the change in slope, we can find the slope at point B (knowing that $\theta_A = 0$):
\begin{align*} \theta_B &= \theta_A + \theta_{B/A} \\ \theta_B &= \theta_{B/A} \end{align*}
Of course, the end at point A did not have to be fixed in order for us to find the rotation at point B. For any beam, if we know the slope at one location for any reason, then we can find the slope at any other location using the first moment area theorem, unless there is an internal hinge or roller between the two points.
With reference to Figure 5.6 part (b), we know that both the slope and deflection at point A ($\theta_A$ and $\Delta_A$) are 0 (because the fixed end does not permit rotation or deflection). Since the slope of the beam is zero at point A, this provides us with a known reference tangent at A (because of the known slope). This reference tangent is also conveniently the same as the undeformed shape of the structure. This means that the distance between the deformed shape and the reference tangent ($\Delta_{B/A}$) is equal to the distance between the deformed shape and the undeformed shape (the deflection $\Delta_{B}$):
\begin{equation*} \Delta_{B} = \Delta_{B/A} \end{equation*}
but only if the reference tangent is at a fixed end where the rotation is zero.
Therefore, if we know a reference tangent that is a zero-slope line (because we know the slope is zero at some point), then we can find the deflection at any other point in a single step using the second moment area theorem as shown in Figure 5.6 part (b). Using the second moment area theorem as described previously in Second Moment Area Theorem, we can find the deflection at point B relative to the reference tangent at point A. Recall that moments of the areas under the curvature diagram must be taken about the deflected point (not the point for the reference tangent):
\begin{align*} \Delta_{B/A} &= A_1 \bar{x}_1 + A_2 \bar{x}_2 \\ \Delta_{B} &= \Delta_{B/A} \end{align*}
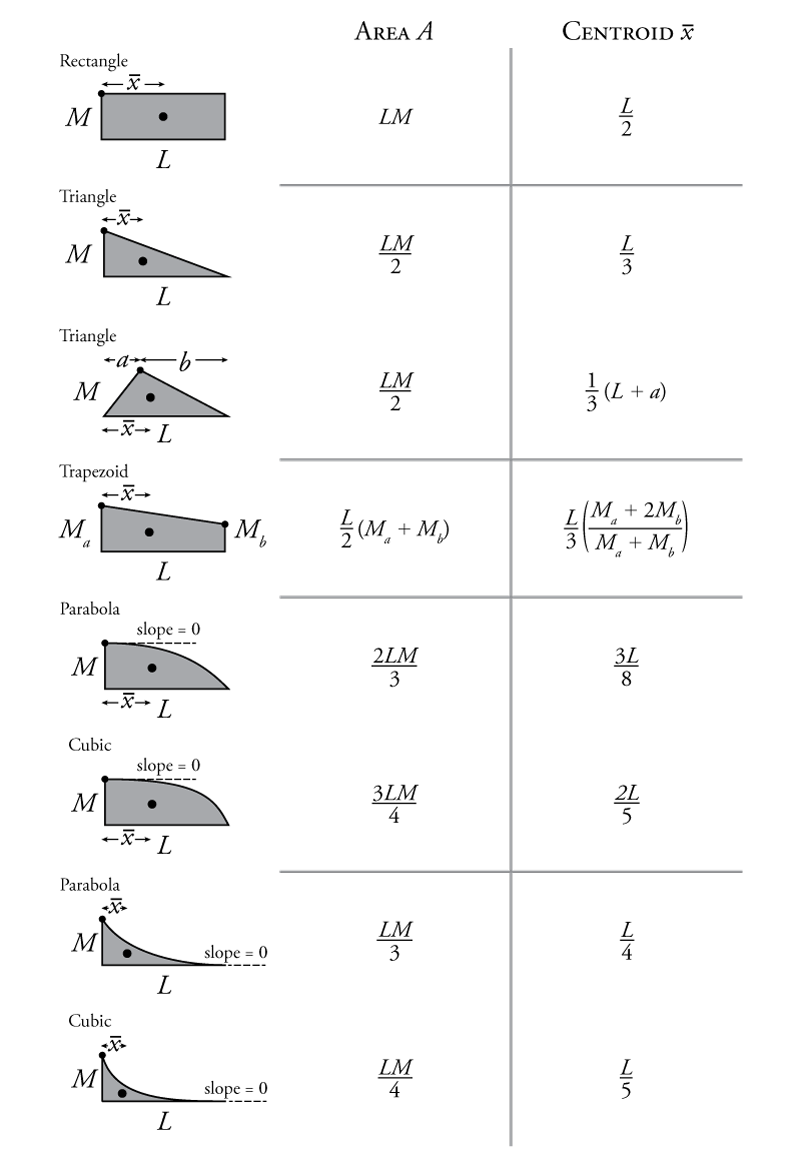
Common equations for calculating the area and centroid of different shapes may be seen in Figure 5.7.
Deflections are Known at Two Points
It is not actually very common that we do know that the slope and deflection are zero at a single point. So, we need some strategy for finding slopes and deflections using the moment area theorems for a wider range of circumstances.
If we want to find deflections using the moment area theorems, then it is obviously important that we have some known reference tangent. Likewise, if you want to find a beam slope using the first moment area theorem, you also need to know the slope some other point on the beam. If we knew the slope somewhere along the beam, that slope could also be used as a reference tangent for deflections.
The first step in most moment area theorem problems is to find a reference tangent with a known slope. If one does not exist at the start of the question, we need to use the moment area theorems to find the slope of a reference tangent before continuing to find other slopes and deflections.
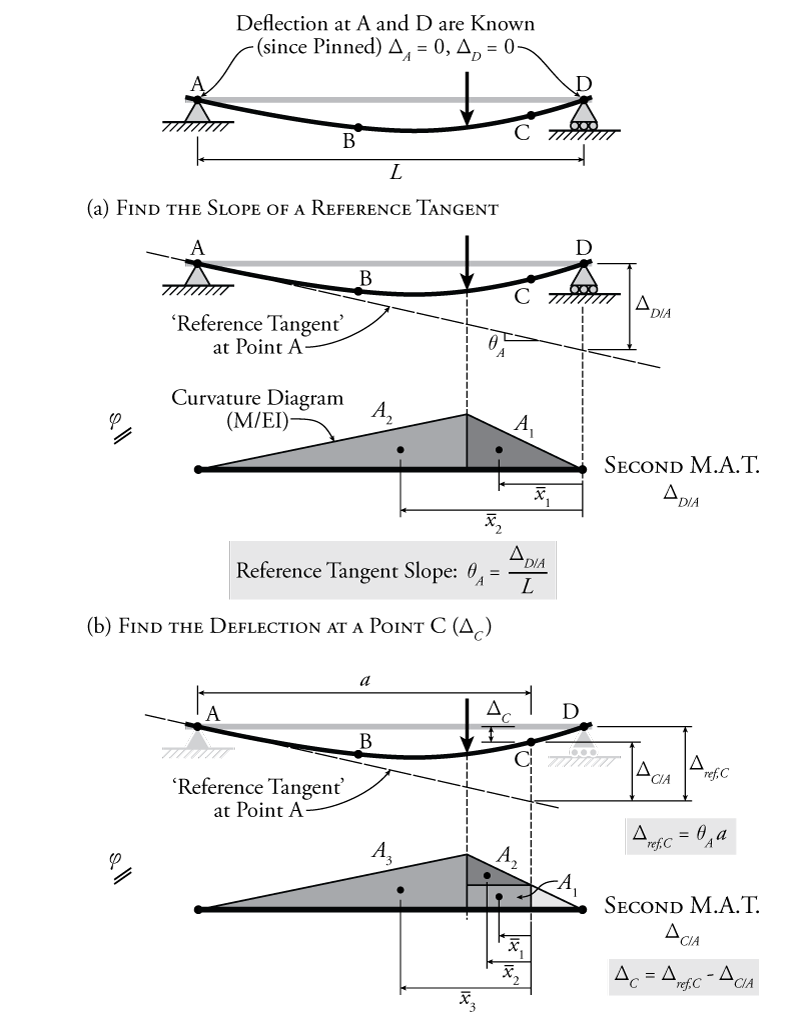
Once such situation is shown in Figure 5.8. This is a very common analysis situation: a simply supported beam. To start with, we don't know the slope at any point along the beam; however, we do happen to know the deflection of the beam at two points. We know that the deflection is zero at both vertical supports (points A and D in Figure 5.8).
If we know the deflection of the beam is zero at two different points, then we can find a reference tangent using the second moment area theorem as shown in Figure 5.8 part (a). We do this by taking advantage of the fact that if the deflection is zero at a point, then the deviation of the reference tangent at that point from the deflected shape will be simply equal to the distance of the reference tangent from the undeformed beam location. The first step is to find the distance between the deformed shape of the beam at one zero deflection point (point D) and the tangent to the beam at the other zero deflection point (point A). Since we know that point D cannot deflect, this distance ($\Delta_{D/A}$) also happens to be equal to the distance between the tangent at A (which will become our reference tangent) and the undeformed shape of the beam. For the example beam shown in Figure 5.8, the second moment area theorem calculation for $\Delta_{D/A}$ is:
\begin{align*} \Delta_{D/A} = A_1 \bar{x}_1 + A_2 \bar{x}_2 \end{align*}
for the two triangles shown in part (a).
Since we now know the distance between the reference tangent (tangent to point A) and the undeformed shape of the beam at point D (zero), then we can find the slope of the reference tangent easily (slope in radians is rise over run, where the run is the length of the beam between points A and D):
\begin{align*} \theta_A = \frac{\Delta_{D/A}}{L} \end{align*}
This angle $\theta_A$ completely defines the slope of our reference tangent.
If we now wanted to find the slope at point C, for example, we could use the first moment area theorem to find $\theta_{C/A}$ (simply the area under the curvature diagram between those two points) and find the slope at C relative to the slope at A:
\begin{align*} \theta_C = \theta_A + \theta_{C/A} \end{align*}
Finding the deflection at a different point on the beam is a bit more complex, but once we have the reference tangent as described above, then we are halfway there. The process required to find the deflection at point C for the sample beam is shown in Figure 5.8 part (b). Recall that the second moment area theorem only gives us the vertical distance between a reference tangent from one point and the deformed shape at another point. In this case, at point C it will give us $\Delta_{C/A}$ as shown in the figure as follows:
\begin{align*} \Delta_{C/A} = A_1 \bar{x}_1 + A_2 \bar{x}_2 + A_3 \bar{x}_3 \end{align*}
This is not a particularly useful result on its own though. What we really want to find is the deflection at point C ($\Delta_C$ in Figure 5.8 part (b)) which is the distance between the deformed shape and the undeformed shape at point C. To find this, the secret is that we first need to know the total distance between the reference tangent (tangent to point A) and the undeformed shape at location C (whereas we currently only have $\Delta_{C/A}$ which is the distance to the deformed shape via the second moment area theorem). We can call the total distance between the reference tangent and the undeformed shape $\Delta_{ref,C}$. This total distance is equal to the sum of the two other parameters $\Delta_{C/A}$ and $\Delta_{C}$ as shown in the figure. To find $\Delta_{ref,C}$, we can use the slope of the reference tangent ($\theta_A$) and the horizontal distance between point C and point A (equal to the length $a$ in the figure). This is effectively using rise over run to calculate the rise based on the run and the slope:
\begin{align*} \theta_A &= \frac{\Delta_{ref,C}}{a} \\ \Delta_{ref,C} &= (\theta_A) a \end{align*}
Now that we know values for $\Delta_{C/A}$ and $\Delta_{ref,C}$, we can use the difference between the two to find the actual value that we are interested in calculating $\Delta_C$:
\begin{align*} \Delta_{ref,C} &= \Delta_{C/A} + \Delta_C \\ \Delta_C &= \Delta_{ref,C} - \Delta_{C/A} \end{align*}
This process may be repeated using the same reference tangent at A to find the deflection for other points along the beam.
Note that the case shown in Figure 5.8 is quite simple. More complex cases may involve internal hinges (which will require separate moment area theorem calculation on either side of the hinge), or may benefit from some intuition regarding the shape of the deflected beam.
 Learn About Structures
Learn About Structures