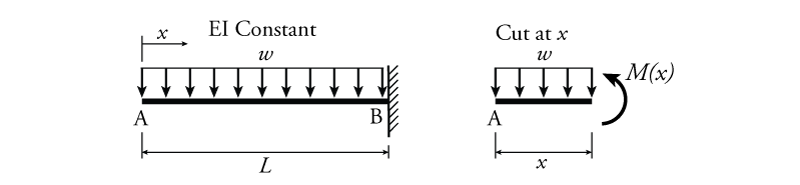Since moment, curvature, slope (rotation) and deflection are related as described by the relationships discussed above, the internal moment may be used to determine the slope and deflection of any beam (as long as the Bernoulli-Euler assumptions are reasonable).
If we know the moment in a beam as a function of the position ($M(x)$), then we can also find the curvature as a function of $x$ using equation \eqref{eq:mom-curv}, which then gives us:
\begin{equation} \boxed {\frac{d^2\Delta}{dx^2} =\frac{d\theta}{dx} \approx \frac{M}{EI} } \label{eq:mom-curv} \tag{1} \end{equation}
This gives us:
\begin{equation} \phi(x) = \frac{M(x)}{E(x)I(x)} \tag{2} \end{equation}
Note that while moment will always be a function of $x$, it is also possible for the moment of inertia ($I$) and the material Young's modulus ($E$) to also vary along the length of the beam.
Knowing the curvature $\phi$ as a function of the moment, we can, as shown in equation \eqref{eq:mom-curv}, integrate once to find the rotation (slope) as a function of the location along the beam $x$, and twice to find the deflection as a function of $x$:
\begin{equation} \boxed{ \theta(x) = \int \phi(x) \, dx = \int \frac{M(x)}{E(x)I(x)} \, dx } \label{eq:curv-slope} \tag{3} \end{equation} \begin{equation} \boxed{ \Delta(x) = \int \theta(x) \, dx = \iint \frac{M(x)}{E(x)I(x)} \, dx^2 } \label{eq:slope-defl} \tag{4} \end{equation}
This process will result in constants of integration, which must be solved for by applying known displacement or rotation boundary conditions.
Example
The integration process will be illustrated using the example cantilever beam shown in Figure 5.3. For this beam, $x=0$ is located at the free end of the cantilever on the left, and therefore $x=L$ at the fixed end on the right. The entirety of the beam is made of a single material and has a constant cross-section, so $E$ and $I$ are constant (i.e. neither is a function of $x$).
The first step is to find an expression for the moment as a function of $x$ so that we can integrate it. This may be done using the section cut analysis method discussed in Section 4.3. For this structure, the method only requires a single cut which is shown on the right side of Figure 5.3, which results in a moment of:
\begin{align*} \curvearrowleft \sum M &= 0 \\ M(x) + wx \left( \frac{x}{2} \right) &= 0 \\ M(x) &= - \frac{wx^2}{2} \end{align*}
Now, we can find the curvature. Since $EI$ is constant:
\begin{align*} \phi(x) &= \frac{M(x)}{EI} \\ \phi(x) &= -\frac{wx^2}{2EI} \end{align*}
This expression is now integrated once for slope and twice for deflection (not forgetting the constants of integration $C$ and $D$):
\begin{align*} \theta(x) &= \int \phi(x) \, dx \\ \theta(x) &= \int -\frac{wx^2}{2EI} \, dx \\ \theta(x) &= -\frac{wx^3}{6EI} + C \end{align*}
and:
\begin{align*} \Delta(x) &= \int \theta(x) \, dx \\ \Delta(x) &= \int \left( -\frac{wx^3}{6EI} + C \right) \, dx \\ \Delta(x) &= -\frac{wx^4}{24EI} + Cx + D \end{align*}
where $C$ and $D$ are constants of integration. These constants can be eliminated by applying known information about the displacement or rotation boundary conditions. For this cantilever, we know that there is no vertical displacement or rotation at the fixed end (where $x=L$). Therefore:
\begin{align*} \theta(L) = 0, \;\; \Delta(L) = 0 \end{align*}
Subbing these in to the above equations in turn, first for slope:
\begin{align*} \theta(x) &= -\frac{wx^3}{6EI} + C \\ 0 &= -\frac{wL^3}{6EI} + C \\ C &= \frac{wL^3}{6EI} \end{align*}
and then for deflection (including the new value for $C$):
\begin{align*} \Delta(x) &= -\frac{wx^4}{24EI} + Cx + D \\ 0 &= -\frac{wL^4}{24EI} + \left( \frac{wL^3}{6EI} \right) L + D \\ D &= -\frac{wL^4}{8EI} \end{align*}
Putting these solved constants of integration back into the original equations, we get:
\begin{equation*} \theta(x) = -\frac{wx^3}{6EI} + \frac{wL^3}{6EI} \end{equation*} \begin{equation*} \boxed{\theta(x) = \frac{w}{6EI} \left( L^3 - x^3 \right)} \end{equation*} \begin{align*} \Delta(x) &= -\frac{wx^4}{24EI} + \left( \frac{wL^3}{6EI} \right) x - \frac{wL^4}{8EI} \end{align*} \begin{equation*} \boxed{\Delta(x) = -\frac{w}{24EI} \left( x^4 - 4xL^3 + 3L^4 \right) } \end{equation*}
If we would like to now find the maximum slope and displacement of the cantilever (which will occur at the free end), we can easily sub $x=0$ into the equations above, giving:
\begin{align*} \theta(0) &= \frac{wL^3}{6EI} \\ \Delta(0) &= -\frac{wL^4}{8EI} \end{align*}
From this example, which is a very simple structure with a very simple load distribution, you can imagine that the direct integration method can become quite unwieldy as the complexity of the structure increases. Therefore, we need some additional simpler ways to determine slopes and displacements of our structures.
 Learn About Structures
Learn About Structures